题目内容
【题目】某区对即将参加中考的4 000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
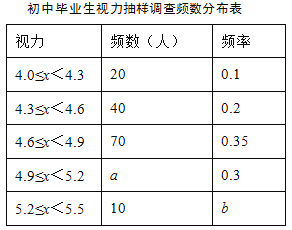
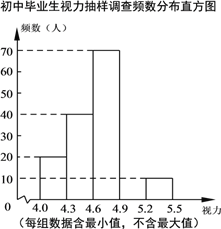
(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?
【答案】(1)200;(2)60,0.05,补图见解析;(3)全区初中毕业生中达到标准视力的学生约有1400人.
【解析】分析:(1)根据视力在4.0≤x<4.3范围内的频数除以频率求出调查的样本容量即可;
(2)由样本容量,根据已知频率或频数求出a与b的值即可;
(3)求出样本中视力正常占的百分比,乘以4000即可得到结果.
详解:(1)根据题意得:20÷0.1=200,即本次调查的样本容量为200,
故答案为:200;
(2)a=200×0.3=60,b=10÷200=0.05,
补全频数分布图,如图所示,
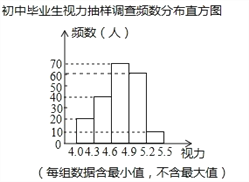
故答案为:60,0.05;
(3)根据题意得:4000×(0.3+0.05)=1400人),
答:全区初中毕业生中达到标准视力的学生约有1400人.

【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.