Question

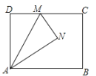
【题目】如图,矩形ABCD中,AB=5,AD=4,M是边CD上一点,将△ADM沿直线AM对折,得△ANM,连BN,若DM=1,则△ABN的面积是（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

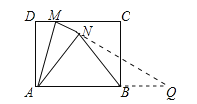
延长MN交AB延长线于点Q，由矩形的性质得出∠DMA=∠MAQ，由折叠性质得出∠DMA=∠AMQ，AN=AD=4，MN=MD=1，得出∠MAQ=∠AMQ，证出MQ=AQ，设NQ=x，则AQ=MQ=1+x，证出∠ANQ=90°，在Rt△ANQ中，由勾股定理得出方程，解方程求出NQ=7.5，AQ=8.5，即可求出△ABN的面积．

解：延长MN交AB延长线于点Q，

∵四边形ABCD是矩形，
∴AB∥DC，
∴∠DMA=∠MAQ，
由折叠性质得：△ANM≌△ADM，
∴∠DMA=∠AMQ，AN=AD=4，MN=MD=1，
∴∠MAQ=∠AMQ，
∴MQ=AQ，
设NQ=x，则AQ=MQ=1+x，
∵∠ANM=90°，
∴∠ANQ=90°，
在Rt△ANQ中，由勾股定理得：AQ2=AN2+NQ2，
∴（x+1）2=42+x2，
解得：x=7.5，
∴NQ=7.5，AQ=8.5，
∵AB=5，AQ=8.5，
∴S△NAB=S△NAQ=×ANNQ=××4×7.5= ；
故选：D．