题目内容
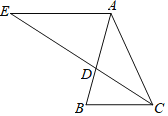
【题目】如图,在△ABC中,AB=AC,∠BAC=36°,CD是∠ACB的平分线交AB于点D,过点A作AE∥BC,交CD的延长线于点E.
(1)求∠ADC的度数;
(2)求证:AE=AC
(3)试问△ADE是等腰三角形吗?请说明理由.
【答案】(1)∠ADC=108°;(2)见解析;(3)△ADE是等腰三角形,理由见解析
【解析】
(1)关键等腰三角形性质和三角形内角和定理求出∠B=∠ACB=72°,求出∠DCB,根据三角形外角性质求出即可;
(2)先判断出∠BCE=∠ACE,再判断出∠BCE=∠E,即可得出结论;
(3)根据平行线求出∠EAD,根据三角形内角和定理求出∠ADE,即可得出答案
解:(1)∵AB=AC,∠BAC=36°,
∴∠B=∠ACB=![]() (180°-∠BAC)=72°,
(180°-∠BAC)=72°,
∵CD是∠ACB的平分线,
∴∠DCB=![]() ∠ACB=36°;
∠ACB=36°;
∴∠ADC=∠B+∠DCB=72°+36°=108°,
(2)AE=AC,证明如下:
∵CD是∠ACB的平分线,
∴∠BCE=∠ACE,
∵AE∥BC,
∴∠BCE=∠E,
∴∠ACE=∠E,
∴AE=AC;
(3)△ADE是等腰三角形,
理由是:∵AE∥BC,
∴∠EAB=∠B=72°,
∵∠B=72°,∠DCB=36°,
∴∠ADE=∠BDC=180°-72°-36°=72°,
∴∠EAD=∠ADE,
∴AE=DE,
即△ADE是等腰三角形.

练习册系列答案
相关题目