题目内容
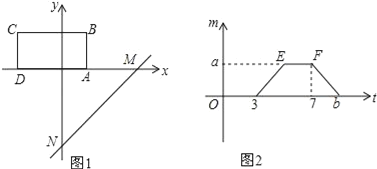
【题目】如图,将矩形ABCD置于平面直角坐标系中,其中AD边在x轴上,AB=2,直线MN:y=x﹣4沿x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被矩形ABCD的边截得的线段长度为m,平移时间为t,m与t的函数图象如图2所示.
(1)点A的坐标为 ,矩形ABCD的面积为 ;
(2)求a,b的值;
(3)在平移过程中,求直线MN扫过矩形ABCD的面积S与t的函数关系式,并写出自变量t的取值范围.
【答案】(1)(1,0),8 ;(2)a=a=2![]() ,b=9;(3)S=
,b=9;(3)S=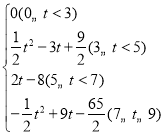 .
.
【解析】
(1)根据直线解析式求出点N的坐标,然后根据函数图象可知直线平移3个单位后经过点A,从而求的点A的坐标,由点F的横坐标可求得点D的坐标,从而可求得AD的长,据此可求得ABCD的面积;
(2)如图1所示;当直线MN经过点B时,直线MN交DA于点E,首先求得点E的坐标,然后利用勾股定理可求得BE的长,从而得到a的值;如图2所示,当直线MN经过点C时,直线MN交x轴于点F,求得直线MN与x轴交点F的坐标从而可求得b的值;
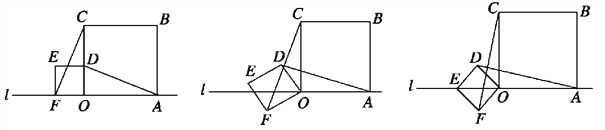
(3)当0≤t<3时,直线MN与矩形没有交点;当3≤t<5时,如图3所示S=△EFA的面积;当5≤t<7时,如图4所示:S=SBEFG+SABG;当7≤t≤9时,如图5所示.S=SABCD﹣SCEF.
解:(1)令直线y=x﹣4的y=0得:x﹣4=0,解得:x=4,
∴点M的坐标为(4,0).
由函数图象可知:当t=3时,直线MN经过点A,
∴点A的坐标为(1,0)
沿x轴的负方向平移3个单位后与矩形ABCD相交于点A,
∵y=x﹣4沿x轴的负方向平移3个单位后直线的解析式是:y=x+3﹣4=x﹣1,
∴点A的坐标为 (1,0);
由函数图象可知:当t=7时,直线MN经过点D,
∴点D的坐标为(﹣3,0).
∴AD=4.
∴矩形ABCD的面积=ABAD=4×2=8.
(2)如图1所示;当直线MN经过点B时,直线MN交DA于点E.
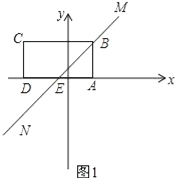
∵点A的坐标为(1,0),
∴点B的坐标为(1,2)
设直线MN的解析式为y=x+c,
将点B的坐标代入得;1+c=2.
∴c=1.
∴直线MN的解析式为y=x+1.
将y=0代入得:x+1=0,解得x=﹣1,
∴点E的坐标为(﹣1,0).
∴BE=![]() .
.
∴a=2![]()
如图2所示,当直线MN经过点C时,直线MN交x轴于点F.
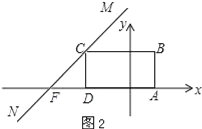
∵点D的坐标为(﹣3,0),
∴点C的坐标为(﹣3,2).
设MN的解析式为y=x+d,将(﹣3,2)代入得:﹣3+d=2,解得d=5.
∴直线MN的解析式为y=x+5.
将y=0代入得x+5=0,解得x=﹣5.
∴点F的坐标为(﹣5,0).
∴b=4﹣(﹣5)=9.
(3)当0≤t<3时,直线MN与矩形没有交点.
∴s=0.
当3≤t<5时,如图3所示;
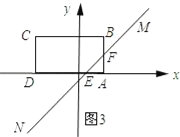
S=![]() ;
;
当5≤t<7时,如图4所示:过点B作BG∥MN.
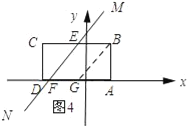
由(2)可知点G的坐标为(﹣1,0).
∴FG=t﹣5.
∴S=SBEFG+SABG=2(t﹣5)+![]() =2t﹣8.
=2t﹣8.
当7≤t≤9时,如图5所示.
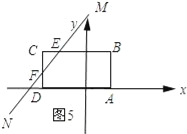
FD=t﹣7,CF=2﹣DF=2﹣(t﹣7)=9﹣t.
S=SABCD﹣SCEF=![]() .
.
综上所述,S与t的函数关系式为S=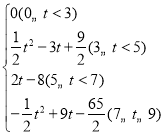

【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数 | 54 | 45 | 30 | 24 | 21 | 12 |
人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.
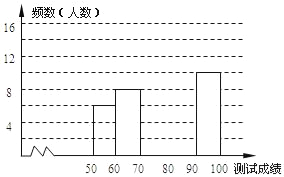
【题目】 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)①表中a的值为 ,中位数在第 组;
②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |