题目内容
【题目】如图，在△ABC中，AB＝4，AC＝3．
（1）试在AB上确定点D的位置，△ACD∽△ABC；
（2）试在AC的延长线上确定点E的位置，使△AEB∽△ABC，此时BE与DC有怎样的位置关系？为什么？
【答案】(1)作图见解析；（2）答案见解析.
【解析】
（1）以CA为边作∠ACD=∠ABC，角的另外一边与AB的交点即为所求；
（2）以BA为边作∠ABE=∠ADC，角的另外一边与AC的延长线的交点即为所求，再进一步根据相似三角形的对应角相等可得答案．
解：（1）如图所示，点D即为所求；
（2）如图所示，点E即为所求；
BE∥DC，
理由：∵△ACD∽△ABC，
∴∠ACD＝∠ABC，
∵△AEB∽△ABC，
∴∠AEB＝∠ABC，
∴∠ACD＝∠AEB，
∴BE∥DC．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
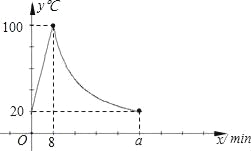
【题目】某小学为每个班级配备了一种可以加热的饮水机，该饮水机的工作程序是：放满水后，接通电源，则自动开始加热，每分钟水温上升10℃，待加热到100℃，饮水机自动停止加热，水温开始下降，水温y（℃）和通电时间x（min）成反比例关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温为20℃，接通电源后，水温和时间的关系如下图所示，回答下列问题：
（1）分别求出当0≤x≤8和8＜x≤a时，y和x之间的关系式；
（2）求出图中a的值；
（3）下表是该小学的作息时间，若同学们希望在上午第一节下课8：20时能喝到不超过40℃的开水，已知第一节下课前无人接水，请直接写出生活委员应该在什么时间或时间段接通饮水机电源．（不可以用上课时间接通饮水机电源）
时间 | 节次 | |
上 午 | 7：20 | 到校 |
7：45～8：20 | 第一节 | |
8：30～9：05 | 第二节 | |
… | … | |
