题目内容
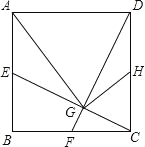
【题目】如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG=![]() AD.其中正确的有( )
AD.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
连接AH,由四边形ABCD是正方形与点E、F、H分别是AB、BC、CD的中点,易证得△BCE≌△CDF与△ADH≌△DCF,根据全等三角形的性质,易证得CE⊥DF与AH⊥DF,根据垂直平分线的性质,即可证得AG=AD,由直角三角形斜边上的中线等于斜边的一半,即可证得HG=![]() AD,根据等腰三角形的性质,即可得∠CHG=∠DAG.则问题得解.
AD,根据等腰三角形的性质,即可得∠CHG=∠DAG.则问题得解.
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=90°,
∵点E、F、H分别是AB、BC、CD的中点,
∴BE=CF,
在△BCE与△CDF中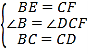 ,
,
∴△BCE≌△CDF,(SAS),
∴∠ECB=∠CDF,
∵∠BCE+∠ECD=90°,
∴∠ECD+∠CDF=90°,
∴∠CGD=90°,
∴CE⊥DF,故①正确;
在Rt△CGD中,H是CD边的中点,
∴HG=![]() CD=
CD=![]() AD,故④正确;
AD,故④正确;
连接AH,
同理可得:AH⊥DF,
∵HG=HD=![]() CD,
CD,
∴DK=GK,
∴AH垂直平分DG,
∴AG=AD,故②正确;
∴∠DAG=2∠DAH,
同理:△ADH≌△DCF,
∴∠DAH=∠CDF,
∵GH=DH,
∴∠HDG=∠HGD,
∴∠GHC=∠HDG+∠HGD=2∠CDF,
∴∠CHG=∠DAG.故③正确.
故选:D.

【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶 | 小瓶 | |
进价(元/瓶) | 5 | 2 |
售价(元/瓶) | 7 | 3 |
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?
【题目】为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表:
零花钱数额 | 人数(频数) | 频率 |
| 6 | 0.15 |
| 12 | 0.30 |
| 16 | 0.40 |
|
| 0.10 |
| 2 |
|

请根据以下图表,解答下列问题:
(1)这次被调查的人数共有__________人,![]() __________;
__________;
(2)计算并补全频数分布直方图;
(3)请估计该校1500名学生中每月零花钱数额低于90的人数.



