题目内容
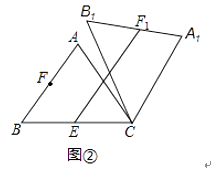
【题目】如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE.若SΔABC=18,△ADF的面积为![]() ,△CFE的面积为
,△CFE的面积为![]() ,则
,则![]()
![]() =________
=________

【答案】3
【解析】
根据D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,S△ABC=18,可以得到S△ADC和S△AEC的面积,再根据图形,即可得到S1-S2的值.
解:∵D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,S△ABC=18,
∴S△ADC=18×![]() =12,S△AEC=18×
=12,S△AEC=18×![]() =9,
=9,
∵S△ADC=S△ADF+S△AFC,S△AEC=S△CEF+S△AFC,
∴S△ADC-S△AEC=S△ADF-S△CEF,
∵S△ADC=12,S△AEC=9,
∴S△ADC-S△AEC=3,
∴S△ADF-S△CEF=3,
∵△ADF的面积为S1,△CEF的面积为S2,
∴S1-S2=3,
故答案为:3.

 阅读快车系列答案
阅读快车系列答案【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
类别 | 时间t(小时) | 人数 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
请根据图表信息解答下列问题: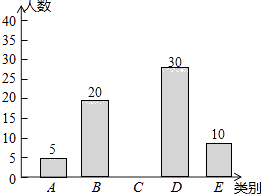
(1)a=;
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
【题目】甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
第一次 | 第二次 | 第三次 | 第四次 | |
甲 | 87 | 95 | 85 | 93 |
乙 | 80 | 80 | 90 | 90 |
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为S甲2=17、S乙2=25,下列说法正确的是( )
A.甲同学四次数学测试成绩的平均数是89分
B.甲同学四次数学测试成绩的中位数是90分
C.乙同学四次数学测试成绩的众数是80分
D.乙同学四次数学测试成绩较稳定