题目内容
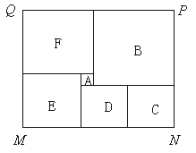
【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
（1）若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出：
正方形F的边长= 米;正方形E的边长= 米;正方形C的边长= 米;
（2）观察图形的特点可知,长方形相对的两边是相等的（如图中的MN=PQ）.根据等量关系可求出x= ;
（3）现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问乙还要多少天完成?甲、乙2个工程队各铺设多少米?
【答案】（1）（x-1），（x-2），（x-3）（2）7（3）乙还要10天完成，甲铺设
m，乙铺设
m
【解析】
（1）根据图象由最小的正方形的边长为1可以得出正方形F、E和C的边长；
（2）设图中最大正方形B的边长是x米，分别表示出QM和PN的值由QM=PN建立方程求出其解即可；
（3）设余下的工程由乙队单独施工，还要y天完成，由工程问题的数量关系建立方程求出其解即可．
解：（1）由题意，得
正方形F的边长（x-1），
正方形E的边长（x-2），
正方形C的边长
或x-3；
故答案是：（x-1），（x-2），（x-3）;
（2）设图中最大正方形B的边长是x米，由图象，得
QM=x-1+x-2，PN=x+，
∵QM=PN，
∴x-1+x-2=x+，
∴x=7．
故答案是：7；
（3）由（1）（2）可知，长方形MNPQ的长为13米，宽为11米，则长方形MNPQ的周长为2×（13+11）=48（米）．
设余下的工程由乙队单独施工，还要y天完成，由题意，得
（
+
）×2+y=1，
解得：y=10．
则甲工程队铺设了
×48=9.6（米）．
乙工程队铺设了48-9.6=38.4（米）．
答：还要10天完成，甲工程队铺设了9.6米，乙工程队铺设了38.4米．
