题目内容
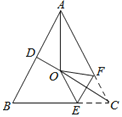
【题目】如图,在矩形纸片ABCD中,AB=6cm,BC=8cm,将矩形纸片折叠,使点C与点A重合,请在图中画出折痕,并求折痕的长.

【答案】图详见解析,折痕长![]() cm.
cm.
【解析】
连接AC,作出AC的垂直平分线,分别交AD、AC、BC于点E、O、F,EF即为折痕;根据勾股定理求出AC的长,根据翻折变换的性质可得AC⊥EF,OA=OC=![]() AC,再利用∠ACB的正切列式求出OF的长,再证明△AOE≌△COF,根据全等三角形对应边相等可得OE=OF,由此即可求得EF的长.
AC,再利用∠ACB的正切列式求出OF的长,再证明△AOE≌△COF,根据全等三角形对应边相等可得OE=OF,由此即可求得EF的长.
如图所示,EF即为折痕;
∵AB=6cm,BC=8cm,
∴由勾股定理可得,AC=10cm,
∵折叠后点C与点A重合,
∴AC⊥EF,OA=OC=![]() AC=
AC=![]() ×10=5cm,
×10=5cm,
∵tan∠ACB=![]() ,
,
∴![]() ,
,
解得OF=![]() cm,
cm,
∵矩形对边AD∥BC,
∴∠OAE=∠OCF,
在△AOE和△COF中,
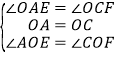 ,
,
∴△AOE≌△COF(ASA),
∴OE=OF=![]() cm,
cm,
∴折痕EF=![]() +
+![]() =
=![]() cm.
cm.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目