题目内容
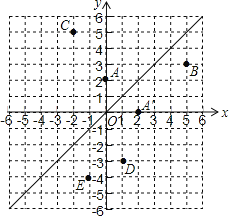
【题目】已知坐标平面内的点A(3,2),B(1,3),C(﹣1,﹣6),D(2a,4a﹣4)中只有一点不在直线l上,则这一点是( )
A.点AB.点BC.点CD.点D
【答案】B
【解析】
先求出直线AB和直线AC的解析式,再把点D(2a,4a-4)分别代入看是否符合即可.
解:设直线AB为y=kx+b,
把点A(3,2),B(1,3)代入得![]() ,
,
解得: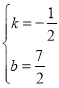 ,
,
即直线AB为:![]()
由x=2a时,![]()
可知,点D不在此函数图象上;
设直线AC为y=mx+n,
把点A(3,2),C(-1,-6)代入得![]() ,
,
解得![]() ,
,
即直线AC为:y=2x-4,
由x=2a时,y=2×2a-4=4a-4可知,点D在此函数图象上;
故A(3,2),C(-1,-6),D(2a,4a-4)在一条直线l上,点B不在直线l上,
故选:B.

练习册系列答案
相关题目
【题目】下表是二次函数y=ax2+bx+c的部分x,y的对应值:
x | … | -1 | - | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | 2 |
| -1 | - | -2 | - | -1 |
| 2 | … |
(1)此二次函数图象的顶点坐标是 ;
(2)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是 。