题目内容
星期一上午班级共有4节课,分别为数学、语文、外语和历史,如果随机排课,那么第一节上数学课,第四节上语文课的概率为( )
A.  B.
B. 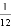 C.
C.  D.
D. 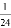
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
题目内容
星期一上午班级共有4节课,分别为数学、语文、外语和历史,如果随机排课,那么第一节上数学课,第四节上语文课的概率为( )
A.  B.
B. 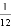 C.
C.  D.
D. 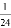
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案