Question

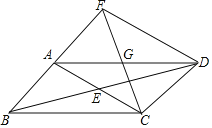
【题目】如图，在矩形ABCD中，AB＝2，BC＝4，把矩形折叠，使点D与点B重合，点C落在点E处，则折痕FG的长为_____．

Answer 1

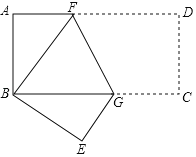
【答案】

【解析】

连接BD，在Rt△ABD中，求得BD的长，在Rt△ABF中运用勾股定理求得BF的长，即可得到DF长，最后在Rt△DOF中求得FO的长，即可得到答案．

解：如图，连接BD，交FG于O，则由轴对称的性质可知，FG垂直平分BD，

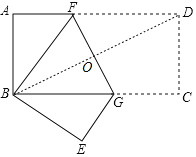
Rt△ABD中，BD＝==，

∴DO＝，

由折叠可得，∠BFO＝∠DFO，

由AD∥BC可得，∠DFO＝∠BGO，

∴∠BFO＝∠BGO，

∴BF＝BG，即△BFG是等腰三角形，

∴BD平分FG，

设BF＝DF＝x，则AF＝4﹣x，

在Rt△ABF中，（4﹣x）2+22＝x2，

解得x＝，即DF＝，

∴Rt△DOF中，OF＝，

∴FG＝2FO＝．

故答案为：．