题目内容
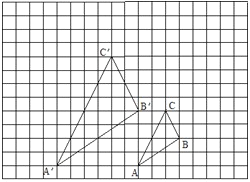
【题目】如图,在△ABC中,∠B=90°,AB=BC=5cm,点Q从点A开始沿AB边向点B以lcm/s的速度移动点P从点B开始沿BC边向点C以2cm/s速度移动,两点同时出发,连接PQ.
(1)经过多长时间后,△PBQ的面积等于4cm2?
(2)△PBQ的面积能否等于7cm2?试说明理由.

【答案】(1)1秒后,△PBQ的面积等于4cm2;(1)△PBQ的面积不能等于7cm2.
【解析】试题(1)点Q从点A开始沿AB边向点B以1cm/s的速度移动,点P从点B开始沿BC边向点C以2cm/s的速度移动,表示出BQ和BP的长度,利用三角形的面积公式可列方程求解.
(2)参照(1)的解法列出方程,根据根的判别式来判断该方程的根的情况.
试题解析:(1)设x秒后,PBQ的面积等于4cm2 ,
此时,AQ=x cm, QB=(5-x)cm. BP=2xcm,
由![]() QB·BP=4得
QB·BP=4得![]() (5-x)·2x=4 ,
(5-x)·2x=4 ,
整理,得x2-5x+4=0,
解得x1=l,x2=4(不合题意,舍去)
所以1秒后,△PBQ的面积等于4cm2 .
(2)根据题意,得![]() (5-x)·2x=7 ,
(5-x)·2x=7 ,
整理,得x2-5x+7=0 ,
因为b2-4ac=25-28<0,
所以此方程无解,即△PBQ的面积不能等于7cm2 .

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目