题目内容
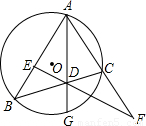
(2001•内江)已知:如图,△ABC内接于⊙O,G是 的中点,连接AG交BC于D,过D的直线交AB于E,交AC的延长线于F;
的中点,连接AG交BC于D,过D的直线交AB于E,交AC的延长线于F;求证:AB•AC-BD•DC=AE•AF-ED•DF.
【答案】分析:在本题中,易证△ABG∽△ADC,从而得出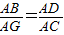 ,即AB•AC=AG•AD,再者根据相交弦定理可知BD•CD=AD•DG,从而利用线段之间的和差关系得出结论.
,即AB•AC=AG•AD,再者根据相交弦定理可知BD•CD=AD•DG,从而利用线段之间的和差关系得出结论.
解答: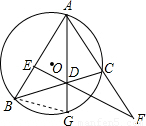 证明:连接BG,
证明:连接BG,
∵∠BAG=∠GAF,∠G=∠ACB,
∴△ABG∽△ADC.
∴AB:AG=AD:AC.
∴AB•AC=AG•AD.
∵BD•CD=AD•DG,
∴AB•AC-BD•CD=AG•AD-AD•DG.
∴AB•AC-BD•CD=AD•(AG-DG).
∵AG-DG=AD,
∴AB•AC-BD•CD=AD2.
同理:AE•AF-ED•DF=AD2.
∴AB•AC-BD•CD=AE•AF-ED•DF.
点评:此题是相似三角形的一个变形,主要考查对应边成比例,把比例式变为等积式.
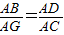 ,即AB•AC=AG•AD,再者根据相交弦定理可知BD•CD=AD•DG,从而利用线段之间的和差关系得出结论.
,即AB•AC=AG•AD,再者根据相交弦定理可知BD•CD=AD•DG,从而利用线段之间的和差关系得出结论.解答:
 证明:连接BG,
证明:连接BG,∵∠BAG=∠GAF,∠G=∠ACB,
∴△ABG∽△ADC.
∴AB:AG=AD:AC.
∴AB•AC=AG•AD.
∵BD•CD=AD•DG,
∴AB•AC-BD•CD=AG•AD-AD•DG.
∴AB•AC-BD•CD=AD•(AG-DG).
∵AG-DG=AD,
∴AB•AC-BD•CD=AD2.
同理:AE•AF-ED•DF=AD2.
∴AB•AC-BD•CD=AE•AF-ED•DF.
点评:此题是相似三角形的一个变形,主要考查对应边成比例,把比例式变为等积式.

练习册系列答案
相关题目
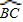 的中点,连接AG交BC于D,过D的直线交AB于E,交AC的延长线于F;
的中点,连接AG交BC于D,过D的直线交AB于E,交AC的延长线于F;

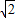 ,AC=3
,AC=3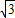 ,D是⊙O上一点,且AD=3,则CD的长应是( )
,D是⊙O上一点,且AD=3,则CD的长应是( )