题目内容
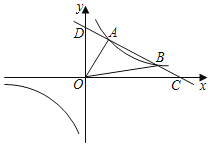
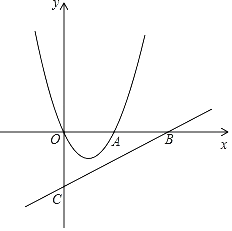
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx经过点A(2,0).直线y=![]() x﹣2与x轴交于点B,与y轴交于点C.
x﹣2与x轴交于点B,与y轴交于点C.
(1)求这条抛物线的表达式和顶点的坐标;
(2)将抛物线y=x2+bx向右平移,使平移后的抛物线经过点B,求平移后抛物线的表达式;
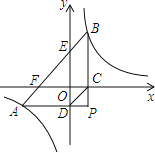
(3)将抛物线y=x2+bx向下平移,使平移后的抛物线交y轴于点D,交线段BC于点P、Q,(点P在点Q右侧),平移后抛物线的顶点为M,如果DP∥x轴,求∠MCP的正弦值.
【答案】(1)y=x2﹣2x,顶点C的坐标是(1,﹣1);(2)y=(x﹣3)2﹣1或y=(x﹣5)2﹣1;(3)![]()
【解析】
(1)根据待定系数法即可求得抛物线的解析式,化成顶点式即可求得顶点坐标;
(2)根据图象上点的坐标特征求得B(4,0),然后分两种情况讨论求得即可;
(3)设向下平移后的抛物线表达式是:y=x2﹣2x+n,得点D(0,n),即可求得P(2,n),代入y=![]() x﹣2求得n=﹣1,即可求得平移后的解析式为y=x2﹣2x﹣1.求得顶点坐标,然后解直角三角形即可求得结论.
x﹣2求得n=﹣1,即可求得平移后的解析式为y=x2﹣2x﹣1.求得顶点坐标,然后解直角三角形即可求得结论.
(1)由题意,抛物线y=x2+bx经过点A(2,0),
得0=4+2b,解得 b=﹣2,
∴抛物线的表达式是y=x2﹣2x.
∵y=x2﹣2x=(x﹣1)2﹣1,
∴它的顶点C的坐标是(1,﹣1).
(2)∵直线![]() 与x轴交于点B,
与x轴交于点B,
∴点B的坐标是(4,0).
①将抛物线y=x2﹣2x向右平移2个单位,使得点A与点B重合,
此时平移后的抛物线表达式是y=(x﹣3)2﹣1.
②将抛物线y=x2﹣2x向右平移4个单位,使得点O与点B重合,
此时平移后的抛物线表达式是y=(x﹣5)2﹣1.
(3)设向下平移后的抛物线表达式是:y=x2﹣2x+n,得点D(0,n).
∵DP∥x轴,
∴点D、P关于抛物线的对称轴直线x=1对称,
∴P(2,n).
∵点P在直线BC上,
∴![]() .
.
∴平移后的抛物线表达式是:y=x2﹣2x﹣1.
∴新抛物线的顶点M的坐标是(1,﹣2).
∴MC∥OB,
∴∠MCP=∠OBC.
在Rt△OBC中,![]() ,
,
由题意得:OC=2,![]() ,
,
∴![]() .
.
即∠MCP的正弦值是![]() .
.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案