题目内容
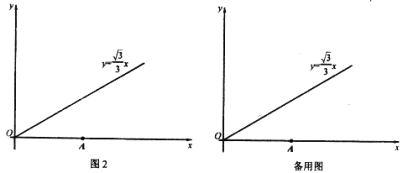
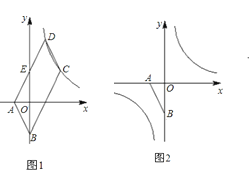
【题目】如图1,已知点A(a,0),B(0,b),且a、b满足![]() , ABCD的边AD与y轴交于点E,且E为AD中点,双曲线
, ABCD的边AD与y轴交于点E,且E为AD中点,双曲线![]() 经过C、D两点.
经过C、D两点.
(1)求k的值;
(2)点P在双曲线![]() 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
【答案】(1)k=4; (2)P(1,4),Q(0,6)或P(-1,-4),Q(0,-6)或P(-1,-4),Q(0,2).
【解析】
(1)先根据非负数的性质求出a、b的值,故可得出A、B两点的坐标,设D(1,t),由DC∥AB,可知C(2,t-2),再根据反比例函数的性质求出t的值即可;
(2)由(1)知k=4可知反比例函数的解析式为y=![]() ,再由点P在双曲线y=
,再由点P在双曲线y=![]() 上,点Q在y轴上,设Q(0,y),P(x,
上,点Q在y轴上,设Q(0,y),P(x,![]() ),再分以AB为边和以AB为对角线两种情况求出x的值,故可得出P、Q的坐标.
),再分以AB为边和以AB为对角线两种情况求出x的值,故可得出P、Q的坐标.
(1)∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴A(-1,0),B(0,-2),
∵E为AD中点,
∴xD=1,
设D(1,t),
又∵DC∥AB,
∴C(2,t-2),
∴t=2t-4,
∴t=4,
∴k=4;
(2)∵由(1)知k=4,
∴反比例函数的解析式为y=![]() ,
,
∵点P在双曲线y=![]() 上,点Q在y轴上,
上,点Q在y轴上,
∴设Q(0,y),P(x,![]() ),
),
①当AB为边时:
如图1,若ABPQ为平行四边形,
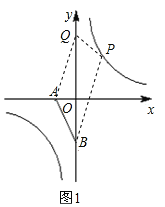
则![]() =0,
=0,
解得x=1,
此时P1(1,4),Q1(0,6);
如图2,若ABQP为平行四边形,
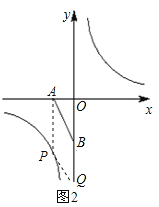
则![]() ,
,
解得x=-1,
此时P2(-1,-4),Q2(0,-6);
②如图3,当AB为对角线时,

AP=BQ,且AP∥BQ;
∴![]() ,
,
解得x=-1,
∴P3(-1,-4),Q3(0,2);
故P1(1,4),Q1(0,6);P2(-1,-4),Q2(0,-6);P3(-1,-4),Q3(0,2);

练习册系列答案
相关题目