题目内容
(1)已知:如图1,线段AB=12cm.点C是线段AB的中点,点 M、N分别是线段AC、BC的中点,求线段MN的长.
(2)已知:如图2,线段AB=a.点C是线段AB上任意一点,若M、N分别是线段AC、BC的中点,则线段MN的长是 .(用含a的式子填空)

(2)已知:如图2,线段AB=a.点C是线段AB上任意一点,若M、N分别是线段AC、BC的中点,则线段MN的长是

分析:(1)根据中点分线段相等,可得AM、MC、CN、BN的关系,可得答案;
(2)根据线段中点分线段相等,可得AM与MC的关系,CN与BN的关系,可得答案.
(2)根据线段中点分线段相等,可得AM与MC的关系,CN与BN的关系,可得答案.
解答:解:(1)因为点C是线段AB的中点,点 M、N分别是
线段AC、BC的中点,
所以点M、C、N是线段AB的四等分点.
所以MC=CN=
AB=
×12=3(cm)
所以MN=MC+CN=6(cm);
(2)∵若M、N分别是线段AC、BC的中点,
∴AM=MC,CN=BN,
AM+CM+CN+NB=a
2(CM+CN)=a
CM+CN=
,
故答案为:
a.
线段AC、BC的中点,
所以点M、C、N是线段AB的四等分点.
所以MC=CN=
| 1 |
| 4 |
| 1 |
| 4 |
所以MN=MC+CN=6(cm);
(2)∵若M、N分别是线段AC、BC的中点,
∴AM=MC,CN=BN,
AM+CM+CN+NB=a
2(CM+CN)=a
CM+CN=
| a |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了两点间的距离,中点分线段相等是解题关键.

练习册系列答案
相关题目
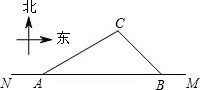 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上.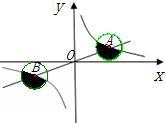 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为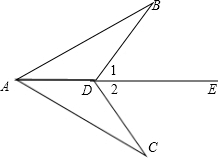 已知,如图,∠1=∠2,
已知,如图,∠1=∠2,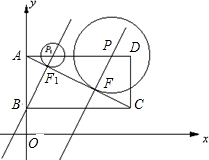 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为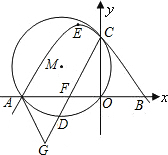 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧