题目内容
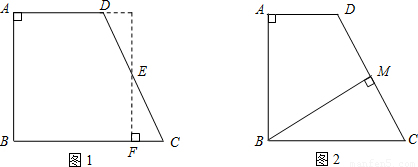
在数学“综合与实践”课中,陈老师要求同学们制作一张直角梯形纸片ABCD,要求梯形的上底AD=3cm,下底BC=5cm.探索:当直角梯形ABCD的高AB是多少厘米时,将该梯形沿某一直线剪成两部分后,能拼成一个既不重叠又无空隙的特殊几何图形.(1)如图1,小颖过腰CD的中点E作EF⊥BC于F,沿EF将梯形剪切后,拼成正方形.求小颖所制作的直角梯形的高AB是多少厘米?
(2)如图2,小亮过点B作BM⊥CD于M,沿BM将梯形剪切后,拼成直角三角形.请在答题卡的相应位置补全拼后的一种直角三角形草图,并求小亮所制作的直角梯形的高AB是多少厘米?
(3)探索当直角梯形的高AB是多少厘米时,将该梯形沿某一直线剪成两部分后,能拼成一个不是正方形的菱形.请在答题卡的相应位置画出两种不同剪切、拼图方法的草图,并直接写出原直角梯形的高AB.
【答案】分析:(1)由拼图可知△DGE≌△CFE,若四边形ABFG是正方形,设DG为x,AG=BF=AB,即3+x=5-x,求出x的值,由AB=AG即可得出结论;
(2)按如图2方式拼接,由拼图可知△GAD≌△BMC,由勾股定理可求出GA的长,由相似三角形的判定定理得出△GAD∽△GMB,故可得出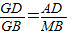 ,即
,即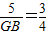 ,求出GB的长,进而可得出AB的长;
,求出GB的长,进而可得出AB的长;
(3)按如图4方式拼接成一个菱形,过点D作DM⊥BC于点M,则AB=DM,由菱形的性质得出CD的长,在Rt△DMC中利用勾股定理可求出DM的长,故可得出结论;按如图5方式拼接成一个菱形,由AD=3cm,BC=5cm可设BM=x,则CM=5-x,ND=MN=3+x,四边形NMCD是菱形可求出x的值,在Rt△OBM中利用勾股定理可求出OB的长,进而可得出AB的长.
解答: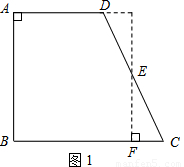 解:(1)∵由拼图可知△DGE≌△CFE,由拼图得,若四边形ABFG是正方形,设DG为x,
解:(1)∵由拼图可知△DGE≌△CFE,由拼图得,若四边形ABFG是正方形,设DG为x,
∴AG=BF=AB,即3+x=5-x,
解得:x=1,
∴AB=AG=3+1=4;
(2)拼法1:按如图2方式拼接,由拼图可知△GAD≌△BMC,
解法一:∵GD=BC=5,由勾股定理可得: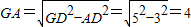
∴BM=AG=4,
∵∠GAD=∠GMB=90°,∠G=∠G,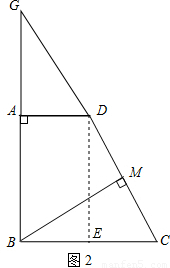
∴△GAD∽△GMB,
∴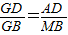 ,即
,即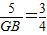 ,
,
解得: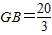 ,
,
∴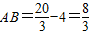 ,
,
解法二:∵CM=AD=3,由勾股定理可得: ,
,
作DE⊥BC于E,得EC=2,
∵∠BMC=∠DEC=90°,
∴tanC=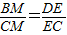 ,
,
∴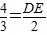 ,
,
∴AB=DE= .
.
拼法2:按如图3方式拼接,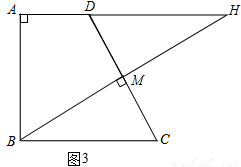
由拼图可知,△HMD≌△BMC,
∴∠HMD+∠BMD=180°,∠HDM+∠ADC=180°,
∴点H是AD与BM延长线的交点,
则HD=BC=5,HM=BM,
∵∠HMD=∠A=90°,
由cosH=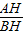 =
=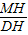 ,即
,即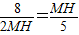 ,解得:
,解得: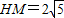 ,
,
∴BH=2HM=4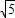 ,
,
由勾股定理可得: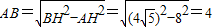 ;
;
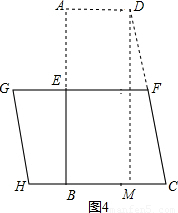
(3)按如图4方式拼接成一个菱形,过点D作DM⊥BC于点M,则AB=DM,
则AD=3,BC=5,四边形GHCF是菱形,
则CH=CF=8,
则MC=CB-AD=5-3=2,DC=2CF=16,
在Rt△DMC中,DM=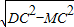 =
=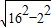 =6
=6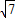 ,即梯形高AB=6
,即梯形高AB=6 cm;
cm;
按如图5方式拼接成一个菱形,
∵AD=3,BC=5,
∴设BM=x,则CM=5-x,ND=MN=3+x,
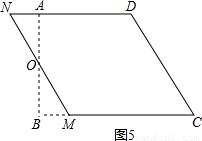 ∵四边形NMCD是菱形,
∵四边形NMCD是菱形,
∴CM=ND=MN,即5-x=3+x,解得x=1,
∴CM=MN=4,
∴OM= MN=2,
MN=2,
在Rt△OBM中,OB=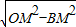 =
=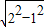 =
=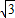 ,
,
∴AB=2OB=2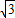 (cm),即梯形高为2
(cm),即梯形高为2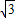 cm.
cm.
点评:本题考查的是相似三角形综合题,涉及到菱形的性质、相似三角形的判定与性质、勾股定理、直角梯形的性质等相关知识,涉及面较广,难度较大.
(2)按如图2方式拼接,由拼图可知△GAD≌△BMC,由勾股定理可求出GA的长,由相似三角形的判定定理得出△GAD∽△GMB,故可得出
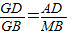 ,即
,即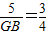 ,求出GB的长,进而可得出AB的长;
,求出GB的长,进而可得出AB的长;(3)按如图4方式拼接成一个菱形,过点D作DM⊥BC于点M,则AB=DM,由菱形的性质得出CD的长,在Rt△DMC中利用勾股定理可求出DM的长,故可得出结论;按如图5方式拼接成一个菱形,由AD=3cm,BC=5cm可设BM=x,则CM=5-x,ND=MN=3+x,四边形NMCD是菱形可求出x的值,在Rt△OBM中利用勾股定理可求出OB的长,进而可得出AB的长.
解答:
 解:(1)∵由拼图可知△DGE≌△CFE,由拼图得,若四边形ABFG是正方形,设DG为x,
解:(1)∵由拼图可知△DGE≌△CFE,由拼图得,若四边形ABFG是正方形,设DG为x,∴AG=BF=AB,即3+x=5-x,
解得:x=1,
∴AB=AG=3+1=4;
(2)拼法1:按如图2方式拼接,由拼图可知△GAD≌△BMC,
解法一:∵GD=BC=5,由勾股定理可得:
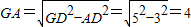
∴BM=AG=4,
∵∠GAD=∠GMB=90°,∠G=∠G,

∴△GAD∽△GMB,
∴
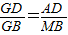 ,即
,即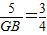 ,
,解得:
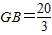 ,
,∴
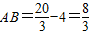 ,
,解法二:∵CM=AD=3,由勾股定理可得:
 ,
,作DE⊥BC于E,得EC=2,
∵∠BMC=∠DEC=90°,
∴tanC=
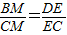 ,
,∴
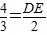 ,
,∴AB=DE=
 .
.拼法2:按如图3方式拼接,

由拼图可知,△HMD≌△BMC,
∴∠HMD+∠BMD=180°,∠HDM+∠ADC=180°,
∴点H是AD与BM延长线的交点,
则HD=BC=5,HM=BM,
∵∠HMD=∠A=90°,
由cosH=
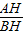 =
=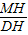 ,即
,即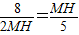 ,解得:
,解得: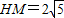 ,
,∴BH=2HM=4
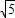 ,
,由勾股定理可得:
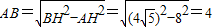 ;
;
(3)按如图4方式拼接成一个菱形,过点D作DM⊥BC于点M,则AB=DM,
则AD=3,BC=5,四边形GHCF是菱形,
则CH=CF=8,
则MC=CB-AD=5-3=2,DC=2CF=16,
在Rt△DMC中,DM=
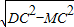 =
=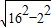 =6
=6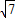 ,即梯形高AB=6
,即梯形高AB=6 cm;
cm; 按如图5方式拼接成一个菱形,
∵AD=3,BC=5,
∴设BM=x,则CM=5-x,ND=MN=3+x,
 ∵四边形NMCD是菱形,
∵四边形NMCD是菱形,∴CM=ND=MN,即5-x=3+x,解得x=1,
∴CM=MN=4,
∴OM=
 MN=2,
MN=2,在Rt△OBM中,OB=
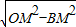 =
=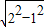 =
=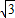 ,
,∴AB=2OB=2
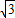 (cm),即梯形高为2
(cm),即梯形高为2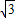 cm.
cm.点评:本题考查的是相似三角形综合题,涉及到菱形的性质、相似三角形的判定与性质、勾股定理、直角梯形的性质等相关知识,涉及面较广,难度较大.

练习册系列答案
相关题目
