题目内容
阅读并回答问题.
求一元二次方程ax2+bx+c=0(a≠0)的根(用配方法).
解:ax2+bx+c=0,
∵a≠0,∴x2+ x+
x+ =0,第一步
=0,第一步
移项得:x2+ x=-
x=- ,第二步
,第二步
两边同时加上( )2,得x2+
)2,得x2+ x+2=-
x+2=- +(
+( )2,第三步
)2,第三步
整理得:(x+ )2=
)2=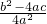 直接开方得x+
直接开方得x+ =±
=±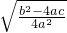 ,第四步
,第四步
∴x=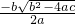 ,
,
∴x1=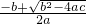 ,x2=
,x2=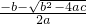 ,第五步
,第五步
上述解题过程是否有错误?若有,说明在第几步,指明产生错误的原因,写出正确的过程;若没有,请说明上述解题过程所用的方法.
解:有错误,在第四步.
错误的原因是在开方时对b2-4ac的值是否是非负数没有进行讨论.
正确步骤为:(x+ )2=
)2=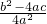 ,
,
①当b2-4ac≥0时,
x+ =±
=±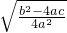 ,
,
x+ =±
=± ,
,
x=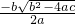 ,
,
∴x1=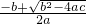 ,x2=
,x2=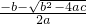 .
.
②当b2-4ac<0时,原方程无解.
分析:①检查原题中的解题过程是否有误:在第四步时,在开方时对b2-4ac的值是否是非负数没有进行讨论;②更正:分类讨论b2-4ac≥0和b2-4ac<0时,原方程的根是什么.
点评:此题属于易错题,学生经常在原题中的第四步出错,即往往漏掉对b2-4ac的值是否是非负数进行讨论,所以,在解题时还是多一份细心好.
错误的原因是在开方时对b2-4ac的值是否是非负数没有进行讨论.
正确步骤为:(x+
 )2=
)2=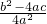 ,
,①当b2-4ac≥0时,
x+
 =±
=±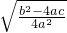 ,
,x+
 =±
=± ,
,x=
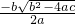 ,
,∴x1=
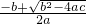 ,x2=
,x2=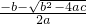 .
.②当b2-4ac<0时,原方程无解.
分析:①检查原题中的解题过程是否有误:在第四步时,在开方时对b2-4ac的值是否是非负数没有进行讨论;②更正:分类讨论b2-4ac≥0和b2-4ac<0时,原方程的根是什么.
点评:此题属于易错题,学生经常在原题中的第四步出错,即往往漏掉对b2-4ac的值是否是非负数进行讨论,所以,在解题时还是多一份细心好.

练习册系列答案
相关题目

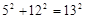 。事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方。如果直角三角形中,两直角边长分别为a、b,斜边长为c,则
。事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方。如果直角三角形中,两直角边长分别为a、b,斜边长为c,则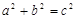 ,这个结论就是著名的勾股定理.
,这个结论就是著名的勾股定理.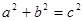 的正整数组(a,b,c)叫勾股数组。例如(3,4,5)就是一组勾股数组。观察下列几组勾股数
的正整数组(a,b,c)叫勾股数组。例如(3,4,5)就是一组勾股数组。观察下列几组勾股数
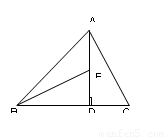
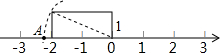
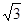 的B点(保留作图痕迹).
的B点(保留作图痕迹).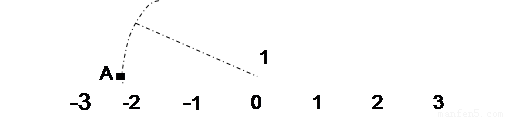
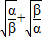 的值.
的值.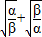 =
=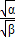 +
+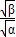 =
=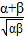 =
= =-3(3)
=-3(3)