题目内容
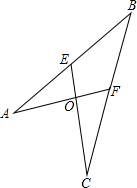如图，AF⊥CE，垂足为点O，AO=CO=2，EO=FO=1．求证：点F为BC的中点．
分析：连接EF、AC，可通过证明EF是三角形ABC的中位线来证明点F为BC的中点．
解答：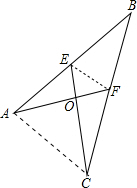
解：连接EF，AC．
∵AO=CO=2，EO=FO=1，
∴
=
=
，
∵∠EOF=∠COA，
∴△EOF∽△COA
∴∠OFE=∠CAO，
∴EF∥AC．
∴△BEF∽△BAC，
∴
=
=
=
，
∴F是BC的中点．
解：连接EF，AC．∵AO=CO=2，EO=FO=1，
∴
| EO |
| OC |
| FO |
| OA |
| 1 |
| 2 |
∵∠EOF=∠COA，
∴△EOF∽△COA
∴∠OFE=∠CAO，
∴EF∥AC．
∴△BEF∽△BAC，
∴
| BF |
| BC |
| EF |
| AC |
| EO |
| OC |
| 1 |
| 2 |
∴F是BC的中点．
点评：本题考查了相似三角形的判定及性质，通过作辅助线即可证明，难度适中．
练习册系列答案
备战中考寒假系列答案
相关题目
上一动点，AK、DC的延长线相交于点F，连接CK、KD．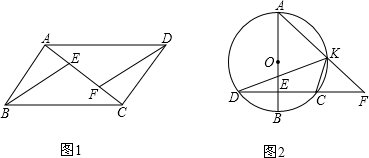
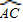上一动点，AK、DC的延长线相交于点F，连接CK、KD．
