题目内容
如果一个点能与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A、B两点可构成直角三角形ABC,则称点C为A、B两点的勾股点.同样,点D也是A、B两点的勾股点.
(1)在矩形ABCD中,AB=12,BC=6,边CD上A,B两点的勾股点的个数为
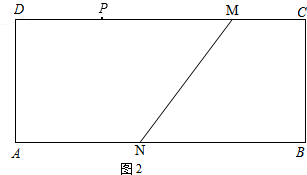
(2)如图1,矩形ABCD中,AB=12,BC=6,DP=4,DM=8,AN=5.过点P作直线l平行于BC,点H为M、N两点的勾股点,且点H在直线l上,求PH的长;
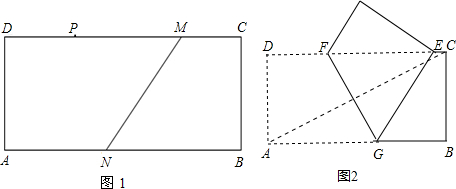
(3)如图2,矩形ABCD中,AB=12,BC=6,将纸片折叠,折痕分别与CD、AB交于点F、G,若A、E两点的勾股点为BC边的中点M,求折痕FG的长.

(1)在矩形ABCD中,AB=12,BC=6,边CD上A,B两点的勾股点的个数为
3
3
个;(2)如图1,矩形ABCD中,AB=12,BC=6,DP=4,DM=8,AN=5.过点P作直线l平行于BC,点H为M、N两点的勾股点,且点H在直线l上,求PH的长;
(3)如图2,矩形ABCD中,AB=12,BC=6,将纸片折叠,折痕分别与CD、AB交于点F、G,若A、E两点的勾股点为BC边的中点M,求折痕FG的长.
分析:(1)A,B两点的勾股点有C、D,以及CD的中点;
(2)点H为M、N两点的勾股点,则分∠HNM=90°,∠HMN=90°,∠MHN=90°三种情况进行讨论,依据相似三角形的性质即可求得PH的长;
(3)A、E两点的勾股点为BC边的中点M,则应分∠AEM=90°和∠AME=90°两种情况进行讨论,当∠AEM=90°时,根据勾股定理可以得到AD2+DE2+CE2+CM2=BM2+AB2,设CE=x,即可得到关于x的方程,求得CE的长,然后利用勾股定理求得FG的长;
当∠AME=90°时,由题意得以AE为直径的圆与BC切于点M,设CE=x,则AE=x+12,在Rt△ADE中利用勾股定理即可求得CE的长,从而求得FG的长.
(2)点H为M、N两点的勾股点,则分∠HNM=90°,∠HMN=90°,∠MHN=90°三种情况进行讨论,依据相似三角形的性质即可求得PH的长;
(3)A、E两点的勾股点为BC边的中点M,则应分∠AEM=90°和∠AME=90°两种情况进行讨论,当∠AEM=90°时,根据勾股定理可以得到AD2+DE2+CE2+CM2=BM2+AB2,设CE=x,即可得到关于x的方程,求得CE的长,然后利用勾股定理求得FG的长;
当∠AME=90°时,由题意得以AE为直径的圆与BC切于点M,设CE=x,则AE=x+12,在Rt△ADE中利用勾股定理即可求得CE的长,从而求得FG的长.
解答: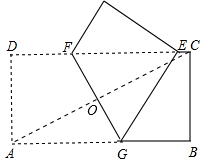 解:(1)A,B两点的勾股点有C、D,以及CD的中点,共3个,
解:(1)A,B两点的勾股点有C、D,以及CD的中点,共3个,
故答案是:3;
(2)当∠HNM=90°时,PH=
;
当∠HMN=90°时,PH=2;
当∠MHN=90°时,
=
,
∴PH=3±
;
(3)当∠AEM=90°时,AD2+DE2+CE2+CM2=AE2+EM2=AM2=BM2+AB2,
设CE=x,则62+(12-x)2+x2+32=32+122,
∴x=6±3
,
∵折痕分别与CD、AB交于点F、G,
∴x=6+3
;
当∠AME=90°时,由题意得以AE为直径的圆与BC切于点M,设CE=x,AE=x+12,
在Rt△ADE中,6+(12-x)2=(12+x)2,
∴CE=
,∴DE=
,AE=
,
∵△ADE∽△FOE,
∴
=
,
∴OF=
,
∴FG=
.
 解:(1)A,B两点的勾股点有C、D,以及CD的中点,共3个,
解:(1)A,B两点的勾股点有C、D,以及CD的中点,共3个,故答案是:3;
(2)当∠HNM=90°时,PH=
| 11 |
| 2 |
当∠HMN=90°时,PH=2;
当∠MHN=90°时,
| 4 |
| PH |
| 6-PH |
| 1 |
∴PH=3±
| 5 |
(3)当∠AEM=90°时,AD2+DE2+CE2+CM2=AE2+EM2=AM2=BM2+AB2,
设CE=x,则62+(12-x)2+x2+32=32+122,
∴x=6±3
| 2 |
∵折痕分别与CD、AB交于点F、G,
∴x=6+3
| 2 |
当∠AME=90°时,由题意得以AE为直径的圆与BC切于点M,设CE=x,AE=x+12,
在Rt△ADE中,6+(12-x)2=(12+x)2,
∴CE=
| 3 |
| 4 |
| 45 |
| 4 |
| 51 |
| 4 |
∵△ADE∽△FOE,
∴
| OF |
| 6 |
| ||
|
∴OF=
| 17 |
| 5 |
∴FG=
| 34 |
| 5 |
点评:本题考查了相似三角形的判定与性质,以及勾股定理,正确根据相似三角形的性质把求线段的长的问题转化成方程问题是关键,体现了方程思想的应用.

练习册系列答案
相关题目