题目内容
【题目】求证:角平分线上的点到这个角的两边距离相等. 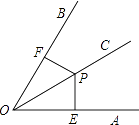
【答案】证明:∵OC平分∠AOB, ∴∠POE=∠POF,
∵PE⊥OA于E,PF⊥OB于F,
∴∠PEO=∠PFO=90°,
在△PEO和△PFO中
∴△PEO≌△PFO(AAS),
∴PE=PF.
所以角平分线上的点到这个角的两边距离相等
【解析】先写出已知、求证,根据角平分线的定义得到∠POE=∠POF,由垂直的定义得∠PEO=∠PFO=90°,易证得△PEO≌△PFO,根据三角形全等的性质即可得到PE=PF.
【考点精析】认真审题,首先需要了解角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上).

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目