题目内容
下列运算是因式分解,且结果正确的是( )
| A、x2-4=(x-2)(x+2) | ||
| B、(x+1)(x+3)=x2+4x+3 | ||
| C、2m2n-8n3=2n(m2-4n2) | ||
D、x-1=x(1-
|
分析:根据分解因式的定义,把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式,以及利用公式法分解因式分别判断即可得出答案.
解答:解:A.x2-4=(x-2)(x+2)利用平方差公式直接分解,故此选项正确;
B.(x+1)(x+3)=x2+4x+3,是整式的乘法运算,故此选项错误;
C.2m2n-8n3=2n(m2-4n2)=2n(m-2n)(m+2n),原题分解因式不彻底,故此选项错误;
D.x-1=x(1-
),分解因式应在整式范围内分解,故此选项错误.
故选:A.
B.(x+1)(x+3)=x2+4x+3,是整式的乘法运算,故此选项错误;
C.2m2n-8n3=2n(m2-4n2)=2n(m-2n)(m+2n),原题分解因式不彻底,故此选项错误;
D.x-1=x(1-
| 1 |
| x |
故选:A.
点评:此题主要考查了因式分解的意义以及公式法与提取公因式法因式分解,正确把握定义从而分解因式是解题关键.

练习册系列答案
相关题目
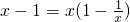
 )
)