题目内容
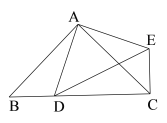
【题目】定义：如果两条线段将一个三角形分成 3个等腰三角形，我们把这两条线段叫做这个三角形的“三分线”．例如：如图①，线段
、
把一个顶角为
的等腰
分成了 3个等腰三角形，则线段、就是等腰的“三分线”．
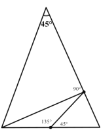
（1）图②是一个顶角为 45°的等腰三角形，在图中画出“三分线”，并标出每个等腰三角形顶角的度数．
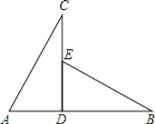
（2）如图③，在
边上取一点
，令
可以分割出第一个等腰，接着又需要考虑如何将
分成2个等腰三角形，即可画出所需要的“三分线”，类比该方法，在图④中画出的“三分线”，并标出每个等腰三角形顶角的度数；
（3）在中，
，
，
．
①画出；（尺规画图，不写作法，保留作图痕迹）
②画出的“三分线”，并做适当的标注．
【答案】（1）见解析；（2）见解析；（3）①见解析；②见解析
【解析】
(1)根据“三分线”的定义，可以分成的三个等腰三角形三个内角度数分别为：45°、45°、90°；22.5°、22.5°、135°；67.5°、67.5°、45°；
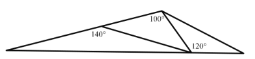
(2)根据“三分线”的定义，可以分成的三个等腰三角形三个内角度数分别为：20°、20°、140°；40°、40°、100°；30°、30°、120°；
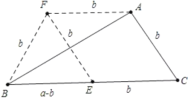
(3)①以a-b、b、b为边作△BEF，，再作边长为b的菱形EFAC（FA∥BE），即可得出△ABC；
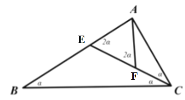
②根据“三分线”的定义，图中△BCE、△AEF、△AFC都是等腰三角形，则线段CE、AF就是“三分线”．
解：(1)如下图,
(2)如下图
(3)①作法：以a-b、b、b为边作△BEF，再作边长为b的菱形EFAC（FA∥BE），如图所示，
②如下图，
练习册系列答案
阅读快车系列答案
相关题目
