题目内容
在半径为r的圆中,圆内接正六边形的边长为
- A.r
- B.
 r
r - C.
 r
r - D.2r
A
分析:画出圆O的内接正六边形ABCDEF,连接OA,OB,得到正三角形AOB,可以求出AB的长.
解答: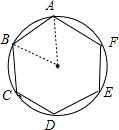 解:如图,ABCDEF是⊙O的内接正六边形,连接OA,OB,
解:如图,ABCDEF是⊙O的内接正六边形,连接OA,OB,
则三角形AOB是等边三角形,所以AB=OA=r.
故选A.
点评:本题考查的是正多边形和圆,连接OA,OB,得到正三角形AOB,就可以求出正六边形的边长.
分析:画出圆O的内接正六边形ABCDEF,连接OA,OB,得到正三角形AOB,可以求出AB的长.
解答:
 解:如图,ABCDEF是⊙O的内接正六边形,连接OA,OB,
解:如图,ABCDEF是⊙O的内接正六边形,连接OA,OB,则三角形AOB是等边三角形,所以AB=OA=r.
故选A.
点评:本题考查的是正多边形和圆,连接OA,OB,得到正三角形AOB,就可以求出正六边形的边长.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
在半径为r的圆中,圆内接正六边形的边长为( )
| A、r | ||
B、
| ||
C、
| ||
| D、2r |
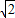 r
r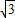 r
r