题目内容
在半径为5的圆中有一点P,且OP=3,则过P的最长弦的长为分析:过点P的最长弦就是直径,最短弦就是垂直于OP的弦,根据垂径定理和勾股定理可求得.
解答: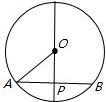 解:过点P的最长弦就是直径,5×2=10,
解:过点P的最长弦就是直径,5×2=10,
最短弦就是垂直于OP的弦,
如图所示,OP⊥AB于P,
∴OA=5,OP=3,
AP=
=
=4,
∴弦AB=2AP=2×4=8.
故答案为:10、8.
 解:过点P的最长弦就是直径,5×2=10,
解:过点P的最长弦就是直径,5×2=10,最短弦就是垂直于OP的弦,
如图所示,OP⊥AB于P,
∴OA=5,OP=3,
AP=
| OA2-OP2 |
| 52-32 |
∴弦AB=2AP=2×4=8.
故答案为:10、8.
点评:本题结合勾股定理考查了垂径定理,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+(
)2成立,知道这三个量中的任意两个,就可以求出另外一个.
| a |
| 2 |

练习册系列答案
相关题目
在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于
,则这个多边形的边数必为( )
| 2 |
| A、7 | B、6 | C、5 | D、4 |