题目内容
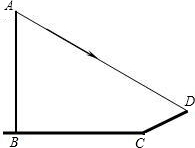
 如图:学校旗杆附近有一斜坡.小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=20米,斜坡坡面上的影长CD=8米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角,求旗杆AB的高度.
如图:学校旗杆附近有一斜坡.小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=20米,斜坡坡面上的影长CD=8米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角,求旗杆AB的高度.
分析:延长AD交BC于E点,则BE即为AB的影长.然后根据物长和影长的比值计算即可.
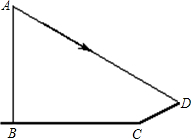
解答: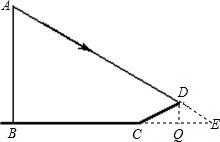 解:延长AD交BC于E点,则∠AEB=30°
解:延长AD交BC于E点,则∠AEB=30°
作DQ⊥BC于Q
在Rt△DCQ中,∠DCQ=30°,DC=8
∴DQ=4,QC=8cos30°=4
在Rt△DQE中,QE=
=4
(米)
∴BE=BC+CQ+QE=20+8
(米)
在Rt△ABE中,AB=BEtan30°=
(米).
答:旗杆的高度约为
米.
 解:延长AD交BC于E点,则∠AEB=30°
解:延长AD交BC于E点,则∠AEB=30°作DQ⊥BC于Q
在Rt△DCQ中,∠DCQ=30°,DC=8
∴DQ=4,QC=8cos30°=4
| 3 |
在Rt△DQE中,QE=
| QD |
| tan30° |
| 3 |
∴BE=BC+CQ+QE=20+8
| 3 |
在Rt△ABE中,AB=BEtan30°=
20
| ||
| 3 |
答:旗杆的高度约为
20
| ||
| 3 |
点评:本题查了解直角三角形的应用.解决本题的关键是作出辅助线得到AB的影长.

练习册系列答案
相关题目
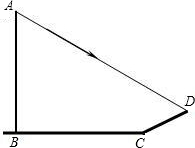 AD与水平地面成26°角,斜坡CD与水平地面BC成30°的角,求旗杆AB的高度(精确到1米).
AD与水平地面成26°角,斜坡CD与水平地面BC成30°的角,求旗杆AB的高度(精确到1米).