题目内容
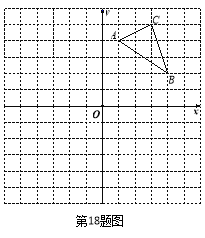
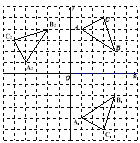
【题目】（辽宁丹东）如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(1，4)，B(4，2)，C(3，5)（每个方格的边长均为1个单位长度）.
（1）请画出△A1B1C1，使△A1B1C1与△ABC关于x轴对称；
（2）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A2B2C2，并直接写出点B旋转到点B2所经过的路径长.
【答案】（1）画图参见解析；（2）画图参见解析，路径长为
π.
【解析】
试题分析：（1）关于x轴对称，点的坐标横坐标不变，纵坐标互为相反数，根据坐标描点连线；（2）连接OA,OB,OC,这三条边绕点O逆时针旋转90度，即旋转角是90度，找到A2，B2，C2，连线即可，点B2所经过的路径长是以O为圆心，OB长为半径的90度的扇形的弧长.利用弧长公式求出即可.
试题解析：(1)∵△A1B1C1与△ABC关于x轴对称,A(1，4)，B(4，2)，C(3，5),∴A1(1，-4),B1(4，-2),C1(3，-5)，连线即可，如图△A1B1C1即为所求；（2)连接OA,OB,OC,这三条边绕点O逆时针旋转90度，得到A2(-4，1),B2(-2，4),C2(-5，3)，将三点连线即可，如图，△A2B2C2即为所求；∵每个方格的边长均为1个单位长度∴点B2所经过的路径长=
=
=π.
练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c图象上部分点的坐标满足下表：
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣3 | ﹣2 | ﹣3 | ﹣6 | ﹣11 | … |
则该函数图象的顶点坐标为（ ）
A.（﹣3，﹣3）
B.（﹣2，﹣2）
C.（﹣1，﹣3）
D.（0，﹣6）
