题目内容
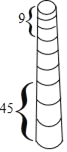
【题目】我国古代的优秀数学著作《九章算术》有一道“竹九节”问题，大意是说：现有﹣一根上细下粗共九节的竹子，自上而下从第2节开始，每一节与前一节的容积之差都相等，且最上面三节的容积共9升，最下面三节的容积共45升，求第五节的容积，及每一节与前一节的容积之差．
请解答上述问题．
【答案】第五节的容积9升，每一节与前一节的容积之差2升．
【解析】
从题目中可知，第2节开始相邻两节的容积差相等设为y，第5节的容积直接设为x，然后根据第5节和容积差建立等量关系：第1节容积+第2节容积+第3节容积＝9，第7节容积+第8节容积+第9节容积＝45构建二元一次方程组求解．
解：设第五节的容积为x升，每一节与前一节的空积之差为y升，依题意得：
，
解得：
，
答：第五节的容积9升，每一节与前一节的容积之差2升．
练习册系列答案
相关题目
