题目内容
【题目】如图，在平面直角坐标系中，⊙A与y轴相切于原点O，平行于x轴的直线交⊙A于M、M两点，若点M的坐标是（-4，-2），则点N的坐标为（ ）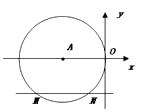
A.（-1，-2）
B.（1，2）
C.（-1．5，-2）
D.（1．5，-2）
【答案】A
【解析】如图：分别过点M、N作x轴的垂线，过点A作AB⊥MN，连接AN，
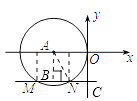
设⊙A的半径为r．
则AN=OA=r，AB=2，
∵AB⊥MN，∴BM=BN，
∴BN=BM=4-r；
则在Rt△ABN中，根据勾股定理，得AB2+BN2=AN2，
即：22+（4-r）2=r2，解得r=2．5，
所以BM=BN=4-2．5=1．5，则N到y轴的距离为2．5-1．5=1，
又∵点N在第三象限，∴N的坐标为（-1，-2）
所以答案是：A．
【考点精析】关于本题考查的勾股定理的概念和垂径定理，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧才能得出正确答案．
练习册系列答案
相关题目
【题目】如图，将一张正方形纸片，剪成四个大小形状一样的小正方形，然后将其中的一个小正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去．
（1）填出下表：
剪的次数 | 1 | 2 | 3 | 4 | 5 | 6 |
正方形个数 |
（2）如果剪了100次，共剪出 个小正方形？
（3）如果剪
次，共剪出 个小正方形？
