题目内容
同学们,学习了无理数之后,我们已经把数的领域扩大到了实数的范围,这说明我们的知识越来越丰富了!可是,无理数究竟是一个什么样的数呢?下面让我们在几个具体的图形中认识一下无理数.
(1) 如图①△ABC 是一个边长为2 的等腰直角三角形,它的面积是2 ,把它沿着斜边的高线剪开拼成如图②的正方形ABCD ,则这个正方形的面积也就等于三角形的面积即为2 ,则这个正方形的边长就是 ,它是一个无理数.
,它是一个无理数.
(1) 如图①△ABC 是一个边长为2 的等腰直角三角形,它的面积是2 ,把它沿着斜边的高线剪开拼成如图②的正方形ABCD ,则这个正方形的面积也就等于三角形的面积即为2 ,则这个正方形的边长就是
 ,它是一个无理数.
,它是一个无理数.
(2)如图,直径为1个单位长度的圆从原点O沿数轴向右滚动一周,圆上的一点P(滚动时与点O重合)由原点到达点O',则OO'的长度就等于圆的周长π,所以数轴上点O'代表的实数就是 ,它是一个无理数.

(3) 如图,在Rt△ABC中,∠C=90°,AC=2,BC=1,根据勾股定理可求得AB= ,它是一个无理数.

好了,相信大家对无理数是不是有了更具体的认识了,那么你也试着在图形中作出两个无理数吧:
1、你能在6×8的网格图中(每个小正方形边长均为1),画出一条长为 的线段吗?
的线段吗?
 的线段吗?
的线段吗?
2、学习了实数后,我们知道数轴上的点与实数是一一对应的关系,那么你能在数轴上找到表示﹣ 的点吗?
的点吗?
 的点吗?
的点吗?
|
解:(2)∵OO '的长度就等于圆的周长π, |
  |

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
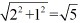 ,
,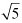 ;
;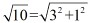 ,
,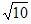 的线段,如右图:
的线段,如右图: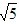 的点.
的点.





 ,它是一个无理数.
,它是一个无理数.
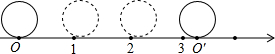

 的线段吗?
的线段吗?
 的点吗?
的点吗?