题目内容
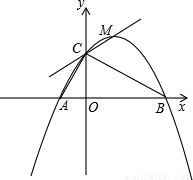
如图14,已知点A(-1,0),B(4,0),点C在y轴的正半轴上,且∠ACB=900,抛物线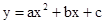 经过A、B、C三点,其顶点为M.
经过A、B、C三点,其顶点为M.
求抛物线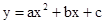 的解析式;
的解析式;
试判断直线CM与以AB为直径的圆的位置关系,并加以证明;
在抛物线上是否存在点N,使得 ?如果存在,那么这样的点有几个?如果不存在,请说明理由。
?如果存在,那么这样的点有几个?如果不存在,请说明理由。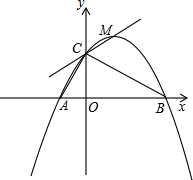
解:(1)Rt△ACB中,OC⊥AB,AO=1,BO=4,
∴△ACO∽△ABO 。∴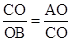 ,∴OC2=OA•OB=4。
,∴OC2=OA•OB=4。
∴OC=2。∴点C(0,2)。
∵抛物线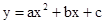 经过A、B两点,
经过A、B两点,
∴设抛物线的解析式为: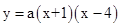 ,将C点代入上式,得:
,将C点代入上式,得: ,解得
,解得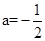 。
。
∴抛物线的解析式: ,即
,即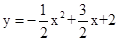 。
。
(2)直线CM与以AB为直径的圆相切。理由如下:
如图,设抛物线的对称轴与x轴的交点为D,连接CD。
由于A、B关于抛物线的对称轴对称,则点D为Rt△ABC斜边AB的中点,CD= AB。
AB。
由(1)知: ,
,
则点M( ),ME=
),ME= 。
。
而CE=OD= ,OC=2,∴ME:CE=OD:OC。
,OC=2,∴ME:CE=OD:OC。
又∵∠MEC=∠COD=90°,∴△COD∽△CEM。∴∠CME=∠CDO。
∴∠CME+∠CDM=∠CDO+∠CDM=90°。∠DCM=90°。
∵CD是⊙D的半径,∴直线CM与以AB为直径的圆相切。
(3)由B(4,0)、C(0,2)得:BC= ,
,
则: 。
。
过点B作BF⊥BC,且使BF=h= ,过F作直线l∥BC交x轴于G。
,过F作直线l∥BC交x轴于G。
Rt△BFG中,sin∠BGF=sin∠CBO= ,
,
BG=BF÷sin∠BGF= 。
。
∴G(0,0)或(8,0)。
易知直线BC:y= x+2,则可设直线l:y=
x+2,则可设直线l:y= x+b,
x+b,
将G点坐标代入,得:b=0或b=4,则:
直线l:y= x或y=
x或y= x+4;
x+4;
联立抛物线的解析式,得: ,或
,或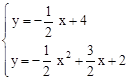 。
。
解得 或
或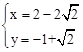 或
或 。
。
∴抛物线上存在点N,使得 ,这样的点有3个:
,这样的点有3个: 。
。
解析

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)
全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)
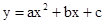 经过A、B、C三点,其顶点为M.
经过A、B、C三点,其顶点为M.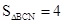 ?如果存在,那么这样的点有几个?如果不存在,请说明理由。
?如果存在,那么这样的点有几个?如果不存在,请说明理由。