题目内容
圆内接正方形的边长为1,则该圆内接正三角形的边长为分析:明确正方形外接圆直径为正方形的对角线长,求出对角线长即可求得其外接圆的半径,然后再求内接正三角形的边长即可.
解答: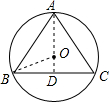 解:正方形外接圆直径为正方形的对角线长.
解:正方形外接圆直径为正方形的对角线长.
∵正方形边长为1,
∴正方形的对角线长为
,
外接圆半径为
.
如图所示:
在Rt△BOD中,OB=
,∠OBD=30°,
∴BD=cos30°×OB=
.
∵BD=CD,
∴BC=2BD=
.
故答案为
.
 解:正方形外接圆直径为正方形的对角线长.
解:正方形外接圆直径为正方形的对角线长.∵正方形边长为1,
∴正方形的对角线长为
| 2 |
外接圆半径为
| ||
| 2 |
如图所示:
在Rt△BOD中,OB=
| ||
| 2 |
∴BD=cos30°×OB=
| ||
| 4 |
∵BD=CD,
∴BC=2BD=
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题主要考查圆锥的计算,解题时根据三角形外接圆半径求其边长.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
圆内接正方形的边长为
cm,则该圆的半径为( )
| 2 |
| A、1cm | ||
B、
| ||
C、
| ||
D、2
|
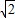 ,则该圆的内接正六边形的边长为 .
,则该圆的内接正六边形的边长为 .