题目内容
已知圆内接正方形的边长为| 2 |
分析:根据已知条件求出该圆的半径,根据正六边形的边长与外接圆半径相等,即可求出.
解答: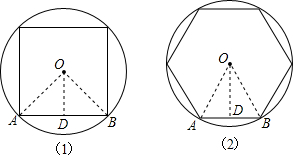 解:如图(1)所示,过O作OD⊥AB于D,连接OA,OB;
解:如图(1)所示,过O作OD⊥AB于D,连接OA,OB;
∵四边形是圆内接四边形,
∴∠AOB=
=90°;
∵OA=OB,OD⊥AB,
∴∠AOD=
=45°,
∴OD=AD=
AB=
,
OA=
=
=1.
如图(2)所示,连接OA,OB,过O作OD⊥AB于D;
∵四边形是圆内接四边形,
∴∠AOB=
=60°,
∵OA=OB,
∴△AOB是正三角形,
∴OA=OB=AB=1.
即该圆的内接正六边形的边长为1.
故答案为:1.
 解:如图(1)所示,过O作OD⊥AB于D,连接OA,OB;
解:如图(1)所示,过O作OD⊥AB于D,连接OA,OB;∵四边形是圆内接四边形,
∴∠AOB=
| 360° |
| 4 |
∵OA=OB,OD⊥AB,
∴∠AOD=
| 90° |
| 2 |
∴OD=AD=
| 1 |
| 2 |
| ||
| 2 |
OA=
| OD2+AD2 |
(
|
如图(2)所示,连接OA,OB,过O作OD⊥AB于D;
∵四边形是圆内接四边形,
∴∠AOB=
| 360° |
| 6 |
∵OA=OB,
∴△AOB是正三角形,
∴OA=OB=AB=1.
即该圆的内接正六边形的边长为1.
故答案为:1.
点评:本题利用了圆内接正方形和圆内接六边形的性质求解.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 ,则该圆的内接正六边形的边长为________.
,则该圆的内接正六边形的边长为________. ,则该圆的内接正六边形的边长为 .
,则该圆的内接正六边形的边长为 .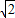 ,则该圆的内接正六边形的边长为 .
,则该圆的内接正六边形的边长为 .