题目内容
【题目】如图,在△ABC中,AB=AC,点D是BC边的中点,点E在AD上,那么下列结论不一定正确的是( )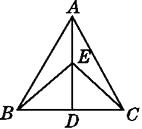
A.AD⊥BC
B.∠EBC=∠ECB
C.∠ABE=∠ACE
D.AE=BE
【答案】D
【解析】解:∵AB=AC,点D是BC边上的中点,
∴AD⊥BC,故A不符合题意;
∴EB=EC,
∴∠EBC=∠ECB,故B不符合题意;
又∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC-∠EBC=∠ACB-∠ECB,即∠ABE=∠ACE,
故C不符合题意;
根据题目条件无法得到∠ABE=∠BAE,
∴AE=BE不一定正确,故D符合题意.
故应选:D 。
根据等腰三角形的三线合一得出AD⊥BC,从而得出AD是BC的中垂线,根据中垂线上的点到线段两端的距离相等,得出EB=EC,根据等边对等角得出∠EBC=∠ECB ,∠ABC=∠ACB ,根据等式的性质得出∠ABE=∠ACE ,从而得出本题答案。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

