题目内容
【题目】某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,求:
(1)此时轮船与小岛P的距离BP是多少海里;
(2)小岛点P方圆3海里内有暗礁,如果轮船继续向东行使,请问轮船有没有触焦的危险?请说明理由.
【答案】
(1)解:∵∠PAB=90﹣75=15°,∠PBA=90°+60°=150°
∴∠APB=180°-∠PAB-∠PBA=15°,
∴∠PAB=∠APB
∴BP=AB=7(海里)
(2)答:没有危险
理由:过点P作PD垂直AC,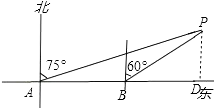
则∠PDB=90°
∴PD= ![]() PB=3.5>3
PB=3.5>3
∴没有危险
【解析】(1)根据方位角的定义得出∠PAB=90﹣75=15°,∠PBA=90°+60°=150° ,根据三角形的内角和得出∠APB=180°-∠PAB-∠PBA=15°,从而判断出∠PAB=∠APB ,根据等角对等边得出BP=AB=7;
(2)没有危险理由:过点P作PD垂直AC ,由∠PBD=90°-60°=30° ,根据含30°角的直角三角形的边之间的关系得出PD的长度,再与3比大小就可以得出结论。

练习册系列答案
相关题目