题目内容
【题目】问题情境:在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,以
的中点,以![]() 为角的顶点作
为角的顶点作![]() .
.
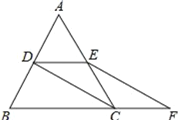
感知易证:(1)如图1,当射线![]() 经过点
经过点![]() 时,
时,![]() 交边
交边![]() 于点
于点![]() .将
.将![]() 从图1中的位置开始,绕点
从图1中的位置开始,绕点![]() 按逆时针方向旋转,使射线
按逆时针方向旋转,使射线![]() 、
、![]() 始终分别交边
始终分别交边![]() ,
,![]() 于点
于点![]() 、
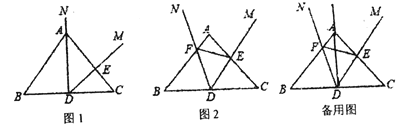
、![]() ,如图2所示,易证
,如图2所示,易证![]() ,则有
,则有![]() .
.
操作探究:(2)如图2,![]() 与
与![]() 是否相似,若相似,请证明;若不相似,请说明理由;
是否相似,若相似,请证明;若不相似,请说明理由;
拓展应用:(3)若![]() ,直接写出当(2)中的旋转角为多少度时,
,直接写出当(2)中的旋转角为多少度时,![]() 与
与![]() 相似.
相似.
【答案】(1)CD;(2)△BDF∽△DEF,理由见详解;(3)10°或40°.
【解析】
(1)如图2,根据∠EDF=∠B及三角形外角性质可得∠BFD=∠CDE,再根据∠B=∠C即可得到△BFD∽△CDE解决问题.
(2)如图2,由(2)得△BFD∽△CDE,则有![]() ,由D是BC的中点可得
,由D是BC的中点可得![]() .再根据∠B=∠EDF即可得到△BDF∽△DEF.
.再根据∠B=∠EDF即可得到△BDF∽△DEF.
(3)由∠B=∠C=50°可得∠BAC=80°,AB=AC,再由BD=CD可得AD⊥BC.若△DEF与△ABC相似,由△BDF∽△DEF可得△BDF与△ABC相似,从而得到∠BDF=∠BAC=80°,或∠BDF=∠C=50°,即可解决问题.
解:(1)如图2,
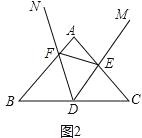
∵AB=AC
∴∠B=∠C,
∵∠FDC是△BFD的一个外角,
∴∠FDC=∠B+∠BFD.
∵∠FDC=∠FDE+∠EDC,∠EDF=∠B,
∴∠BFD=∠CDE.
∵∠B=∠C,
∴△BFD∽△CDE;
∴![]() .
.
(2)如图2,结论:△BDF∽△DEF.

理由:由(1)得![]() .
.
∵D是BC的中点,
∴BD=CD,
∴![]() ,
,
又∵∠B=∠EDF,
∴△BDF∽△DEF.
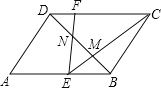
(3)连接AD,如图3,
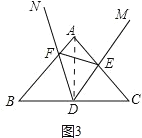
∵∠B=∠C=50°,
∴∠BAC=80°,AB=AC.
∵BD=CD,
∴AD⊥BC.
若△DEF与△ABC相似,
∵△BDF∽△DEF,
∴△BDF与△ABC相似,
∴∠BDF=∠BAC=80°,或∠BDF=∠C=50°,
∴∠ADF=90°﹣80°=10°,或∠ADF=90°﹣50°=40°,
∴当(2)中的旋转角为10°或40°时,△DEF与△ABC相似.

 步步高达标卷系列答案
步步高达标卷系列答案