��Ŀ����
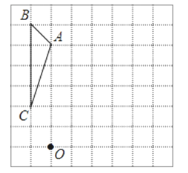
����Ŀ���Ķ�����������ϣ��ش����⣬����һ������ֱ��y��ax+b��ֱ��y��bx+a��Ϊ������ֱ���������磬ֱ��y��x+4��ֱy��4x+1��Ϊ������ֱ���������϶�������ƽ��ֱ������ϵ�е���������P1��x1��y1����P2��x2��y2����P1��P2������ֱ�Ǿ���d��P1��P2����|x1��x2|+|y1��y2|���磺Q1����3��1����Q2��2��4��������ֱ�Ǿ���Ϊd��Q1��Q2����|��3��2|+|1��4|��8������������P0��x0��y0��Ϊһ�����㣬Q��x��y����ֱ��y��ax+b�ϵĶ��㣬���ǰ�d��P0��Q������Сֵ����P0��ֱ��y��ax+b��ֱ�Ǿ��룮
��1������S����1��6����T����2��3��������ֱ�Ǿ���d��S��T������ ����
��2��ֱ��y����2x+3�ϵ�һ��H��a��b����������������ֱ�����ϵĵ㣬���H�����꣮
��3������ֱ��y��ax+b�ϵ�����һ��M��m��n�������е�N��3m��2m��3n��������������ֱ�����ϣ������L��5����1����ֱ��y��ax+b��ֱ�Ǿ��룮
���𰸡���1��4����2����H��1��1������3��5![]()
��������
��1������������ֱ�Ǿ��빫ʽ���ɵã�
��2���ȸ���������ֱ�����Ķ���ó�����ֱ�ߵĽ���ʽ����������⼴�ɵã�
��3���ȸ���������ֱ�����Ķ���ó�����ֱ�ߵĽ���ʽ���ٸ��ݵ�M��N������ɵ�һ������a��b�ķ����飬��������������һ��M�������������a��b��ֵ���Ӷ��ɵ�ֱ��![]() �Ľ���ʽ��Ȼ����ݵ㵽ֱ�ߵ�ֱ�Ǿ���Ķ��弴�ɵã�
�Ľ���ʽ��Ȼ����ݵ㵽ֱ�ߵ�ֱ�Ǿ���Ķ��弴�ɵã�
��1����������ֱ�Ǿ��빫ʽ�ã�![]()
�ʴ�Ϊ��4��
��2��ֱ��![]() ��������ֱ����Ϊ
��������ֱ����Ϊ![]()
����![]() �����
�����![]()
���H������Ϊ![]() ��
��
��3��ֱ��![]() ��������ֱ����Ϊ
��������ֱ����Ϊ![]()
������ã�![]()
���![]()
��������һ��![]() ��������ʽ������
��������ʽ������
��![]() �����
�����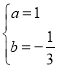
��ˣ�ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]()
���![]() ��ֱ��
��ֱ��![]() �Ķ���
�Ķ���
��![]()
��![]() ʱ��
ʱ��![]()
��![]() ʱ��
ʱ��![]()
��![]() ʱ��
ʱ��![]()
���ϣ�![]() ����СֵΪ
����СֵΪ![]()
���![]() ��ֱ��
��ֱ��![]() ��ֱ�Ǿ���Ϊ
��ֱ�Ǿ���Ϊ![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�