题目内容
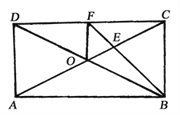
【题目】如图,已知矩形ABCD的对角线AC、BD交于O点,∠ABC的平分线交AC于E,交CD于F,∠DBF=15°,连结OF,则下列三角形①△AOD,②△COF,③△DOF,④△EOF中是等腰三角形的为________(填入序号)。
【答案】①②④
【解析】试题分析:根据矩形的对角线互相平分且相等,可知OA=OD=OB=OC,所以①△AOD是等腰三角形;由BF平分∠ABC,∠DBF=15°,可求得∠CFB=∠CBF=∠FBA=45°,因此可知∠ABD=30°,所以可知△BOC是等边三角形,由此可知BC=CF=OB=OC,可知②△COF为等腰三角形,由三角形的外角的性质,可知∠FEO=∠OCD+∠CFE=75°,因为CF=CO,∠FCO=30°,所以可得∠COF=75°,因此可知OF=EF,所以④△EOF是等腰三角形.
故答案为:①②④.

练习册系列答案
相关题目
【题目】小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | a | 40% |
1200≤x<1400 | 9 | 22.5% |
1400≤x<1600 | b | c |
1600≤x<1800 | 2 | 5% |
合计 | 40 | 100% |
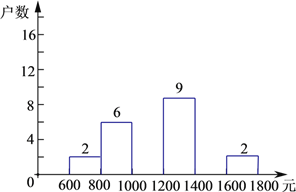
根据以上提供的信息,解答下列问题:
(1)频数分布表中:a= ,b= ,c= .
(2)补全频数分布直方图.
(3)请估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?