题目内容
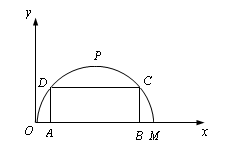
 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式.
分析:(1)利用现以O点为原点,抛物线最大高度为6米,底部宽度OM为12米,得出点M及抛物线顶点P的坐标即可;
(2)利用顶点式将P点M点代入求出抛物线解析式即可.
(2)利用顶点式将P点M点代入求出抛物线解析式即可.
解答:解:(1)∵其最大高度为6米,底部宽度OM为12米,
∴点M及抛物线顶点P的坐标分别为:M(12,0),P(6,6).
(2)设抛物线解析式为:y=a(x-6)2+6,
∵抛物线y=a(x-6)2+6经过点(0,0),
∴0=a(0-6)2+6,即a=-
,
∴抛物线解析式为:y=-
(x-6)2+6,即y=-
x2+2x.
∴点M及抛物线顶点P的坐标分别为:M(12,0),P(6,6).
(2)设抛物线解析式为:y=a(x-6)2+6,
∵抛物线y=a(x-6)2+6经过点(0,0),
∴0=a(0-6)2+6,即a=-
| 1 |
| 6 |
∴抛物线解析式为:y=-
| 1 |
| 6 |
| 1 |
| 6 |
点评:此题主要考查了顶点式求二次函数解析式,利用数形结合得出抛物线解析式是解题关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
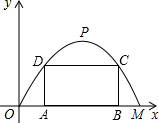 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.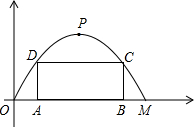 如图,某公路隧道横截面为抛物线,其最大高度6米,底部宽度OM为12米,现以O点为原点,OM所在的直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度6米,底部宽度OM为12米,现以O点为原点,OM所在的直线为x轴建立直角坐标系.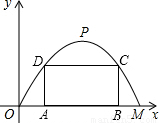 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.