题目内容
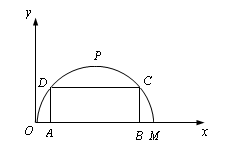
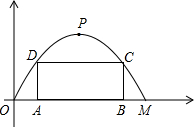 如图,某公路隧道横截面为抛物线,其最大高度6米,底部宽度OM为12米,现以O点为原点,OM所在的直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度6米,底部宽度OM为12米,现以O点为原点,OM所在的直线为x轴建立直角坐标系.(1)求这条抛物线的解析式(不必写x的取值范围);
(2)若要搭建一个矩形支架AD-DC-CB(由三段组成)使C、D在抛物线上,A、B在地面OM上,则这个支架总长L的最大值是多少米?
分析:(1)先根据所建坐标系求出顶点P的坐标,再设解析式为顶点式,把原点O的坐标代入,运用待定系数即可求出解析式;
(2)总长由三部分组成,根据它们之间的关系可设A点坐标为(m,0),用含m的式子表示三段的长,再求其和的表达式,然后运用函数的性质求解.
(2)总长由三部分组成,根据它们之间的关系可设A点坐标为(m,0),用含m的式子表示三段的长,再求其和的表达式,然后运用函数的性质求解.
解答:解:(1)∵某公路隧道横截面为抛物线,其最大高度6米,
∴顶点P的纵坐标为6,
又∵底部宽度OM为12米,
∴顶点P的横坐标也为6,
∴P(6,6).
设抛物线的解析式为:y=a(x-6)2+6.
∵抛物线y=a(x-6)2+6经过点(0,0),
∴0=a(0-6)2+6,解得a=-
.
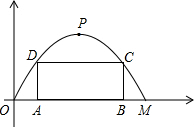 ∴抛物线解析式为:y=-
∴抛物线解析式为:y=-
(x-6)2+6,即y=-
x2+2x;
(2)设A(m,0),则B(12-m,0),C(12-m,-
m2+2m),D(m,-
m2+2m).
则“支撑架”总长:AD+DC+CB=(-
m2+2m)+(12-2m)+(-
m2+2m)
=-
m2+2m+12
=-
(m-3)2+15.
∵此二次函数的图象开口向下.
∴当m=3米时,AD+DC+CB有最大值为15米.
∴顶点P的纵坐标为6,
又∵底部宽度OM为12米,
∴顶点P的横坐标也为6,
∴P(6,6).
设抛物线的解析式为:y=a(x-6)2+6.
∵抛物线y=a(x-6)2+6经过点(0,0),
∴0=a(0-6)2+6,解得a=-
| 1 |
| 6 |
 ∴抛物线解析式为:y=-
∴抛物线解析式为:y=-| 1 |
| 6 |
| 1 |
| 6 |
(2)设A(m,0),则B(12-m,0),C(12-m,-
| 1 |
| 6 |
| 1 |
| 6 |
则“支撑架”总长:AD+DC+CB=(-
| 1 |
| 6 |
| 1 |
| 6 |
=-
| 1 |
| 3 |
=-
| 1 |
| 3 |
∵此二次函数的图象开口向下.
∴当m=3米时,AD+DC+CB有最大值为15米.
点评:本题考查了二次函数的应用,难度在第(2)问,要分别求出三部分的表达式再求其和.关键在于根据图形特点选取一个合适的参数表示它们,得出关系式后运用函数性质来解.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
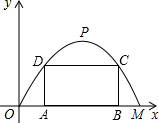 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系. 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.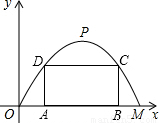 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.