题目内容
【题目】在△ABC中,AD平分∠BAC,BD⊥AD于D,过D作DE∥AC交AB于点E.
(1)求证:E是AB的中点;
(2)若AB=6,求线段DE的长.
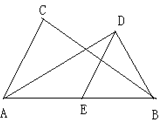
【答案】(1)证明见解析;(2)DE的长为3.
【解析】试题分析:(1)证明∠EAD=∠EDA,此为解题的关键性结论;证明∠EAD=∠EDA,即可解决问题.(2)证明DE为直角△ABD斜边的中线,即可解决问题.
试题解析:(1)证明:∵AD平分∠BAC
∴∠CAD=∠EAD
∵DE∥AC
∴∠CAD=∠ADE
∴∠EAD=∠ADE
∴DE=AE
∵BD⊥AD
∴∠ADB=90
∴∠ADE+∠BDE=90 ,∠EAD+∠ABD=90
∵∠EAD=∠ADE
∴∠BDE=∠ABD
∴BE=DE
∴AE=BE
∴E是AB的中点
(2)解:由(1)知∠ADB=90 , E是AB的中点
∴DE=![]() AB
AB
∵AB=6
∴DE=![]()

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目