题目内容
【题目】某校准备组织290名师生进行野外考察活动,行李共有100件,学校计划租用甲、乙两种型号的汽车共8辆,经了解,甲种汽车每辆最多能载40人(不含司机)和10件行李,乙种汽车每辆最多能载30人(不含司机)和20件行李设租用甲种汽车x辆,请你帮助学校设计所有可能的租车方案.
【答案】共有两种租车方案:方案一:租用甲种汽车5辆,乙种汽车3辆,方案二:租用甲种汽车6辆,乙种汽车2辆
【解析】
设租用甲种汽车x辆,则租用乙种汽车![]() 辆.根据两种汽车载人数量大于等于290,行李数量大于等于100,建立不等式组求解.
辆.根据两种汽车载人数量大于等于290,行李数量大于等于100,建立不等式组求解.
解:设租用甲种汽车x辆,则租用乙种汽车![]() 辆.
辆.
由题意得![]() ,
,
解得![]() .
.
![]() 是整数,
是整数,
![]() 或
或![]() .
.
即共有两种租车方案:
方案一:租用甲种汽车5辆,乙种汽车3辆.
方案二:租用甲种汽车6辆,乙种汽车2辆.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
【题目】数学课上,李老师出示了如下框中的题目.
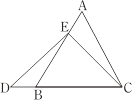
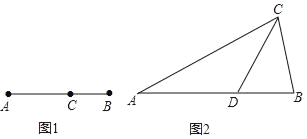
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
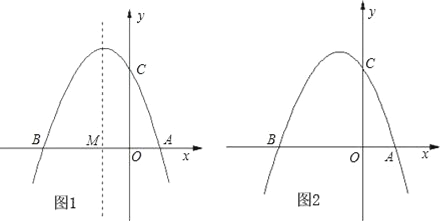
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).