题目内容
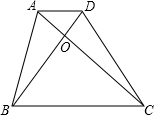 (2013•无锡)如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,AD=1,BC=4,则△AOD与△BOC的面积比等于( )
(2013•无锡)如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,AD=1,BC=4,则△AOD与△BOC的面积比等于( )分析:由梯形ABCD中,AD∥BC,可得△AOD∽△COB,又由AD=1,BC=4,根据相似三角形的面积比等于相似比的平方,即可求得△AOD与△BOC的面积比.
解答:解:∵梯形ABCD中,AD∥BC,
∴△AOD∽△COB,
∵AD=1,BC=4,
即AD:BC=1:4,
∴△AOD与△BOC的面积比等于:1:16.
故选D.
∴△AOD∽△COB,
∵AD=1,BC=4,
即AD:BC=1:4,
∴△AOD与△BOC的面积比等于:1:16.
故选D.
点评:此题考查了相似三角形的判定与性质.此题比较简单,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
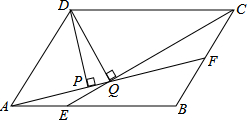 (2013•无锡)如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )
(2013•无锡)如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )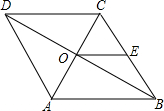 (2013•无锡)如图,菱形ABCD中,对角线AC交BD于O,AB=8,E是CB的中点,则OE的长等于
(2013•无锡)如图,菱形ABCD中,对角线AC交BD于O,AB=8,E是CB的中点,则OE的长等于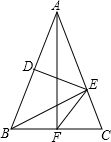 (2013•无锡)如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC=
(2013•无锡)如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC=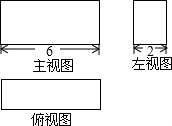 (2013•无锡)如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是
(2013•无锡)如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是