题目内容
【题目】如图，四边形ABCD内接于⊙O，BC是直径，∠BAD=120°，AB=AD．
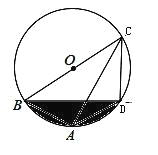
（1）求证：四边形ABCD是等腰梯形；
（2）已知AC=6，求阴影部分的面积．
【答案】（1）见解析 （2）4π－3
【解析】试题分析：（1）根据AB=AD，∠BAD=120°可以得到∠ABD=∠ADB=30°，从而说明弧AB和弧AD的度数为60°，根据BC为直径可以说明弧CD的度数也是60°，从而可以得到AB=CD，然后根据∠CAD=∠ACB=30°得出AD∥BC；（2）阴影部分面积利用扇形面积减去△BOD的面积．
试题解析：（1）∵∠BAD=120°，AB=AD
∴∠ABD=∠ADB=30°
∴弧AB和弧AD的度数都等于60°
又 ∵BC是直径
∴弧CD的度数也是60°
∴AB=CD
∵∠CAD=∠ACB=30°
∴BC∥AD
∴四边形ABCD是等腰梯形．
（2）∵BC是直径
∴∠BAC=90°
∵∠ACB=30°，AC=6
∴BC=
∴r=2
∵弧AB和弧AD的度数都等于60°
∴∠BOD=120°
连接OA交BD于点E，则OA⊥BD
∴OE=OB×sin30°=BE=0B×cos30°=3 BD=2BE=6
∴
=
=4π－3．
【题目】目前
节能灯在城市已基本普及，为面向乡镇市场，苏宁电器分店决定用76000元购进室内用、室外用节能灯，已知这两种类型的节能灯进价、售价如下：
价格 类型 | 进价（元/盏） | 售价（元/盏） |
室内用节能灯 | 40 | 58 |
室外用节能灯 | 50 | 70 |
（1）若该分店共购进节能灯1700盏，问购进的室内用、室外用节能灯各多少盏？
（2）若该分店将进货全部售完后获利要不少于32000元，问至少需要购进多少盏室内用节能灯？
（3）挂职锻炼的大学生村官王祥自酬了4650元在该分店购买这两种类型的节能灯若干盏，分发给村民使用，其中室内用节能灯盏数不少于室内用节能灯盏数的2倍，问王祥最多购买室外用节能灯多少盏？
