题目内容
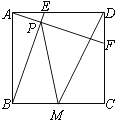
【题目】如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为.
【答案】![]() .
.
【解析】试题分析:本题主要考查的是最短路径问题,由轴对称图形的性质和正方形的性质确定出点P的位置是解题的关键.首先作出点D关于BC的对称点D′,从而可知当点P、M、D′在一条直线上时,路径最短,当点E与点D重合,点F与点C重合时,PG和GD′均最短,即PD′最短,然后由正方形的性质和轴对称图形的性质可知:PG=2,GD′=6,最后由勾股定理即可求得PD′的长,从而可求得MD+MP的最小值.
如图作点D关于BC的对称点D′,连接PD′,由轴对称的性质可知:MD=D′M,CD=CD′=4,
∴PM+DM=PM+MD′=PD′,过点P作PG垂直于C,垂足为G,易证AF⊥BE,故可知P的轨迹为以AB为直径的四分之一圆弧,当点E与点D重合,点F与点C重合时,PG和GD′均最短, ∴此时PD′最短.
∵四边形ABCD为正方形,
∴PG=![]() AD=2,GC=
AD=2,GC=![]() DC=2.
DC=2.
∴GD′=6.
在Rt△PGD′中,由勾股定理得:PD′=![]() =
=![]() =2
=2![]() .
.
故答案为2![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目