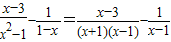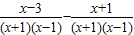题目内容
对于试题:“先化简,再求值:| x-3 |
| x2-1 |
| 1 |
| 1-x |
∵
| x-3 |
| x2-1 |
| 1 |
| 1-x |
| x-3 |
| (x-1)(x+1) |
| 1 |
| x-1 |
=
| x-3 |
| (x-1)(x+1) |
| x+1 |
| (x-1)(x+1) |
=x-3-(x+1)=2x-2,③
∴当x=2时,原式=2×2-2=2. ④
(1)小亮的解答在哪一步开始出现错误:
(2)从②到③是否正确:
(3)请你写出正确的解答过程.
分析:(1)第①步最简公分母是(x+1)(x-1),把1-x变为-(x-1)而第①步没变符号;
(2)第②到③步应按同分母分式的加减法:分母不变,分子相加减.而不应该把分母去掉;
(3)最简公分母为(x+1)(x-1),通分化简即可.
(2)第②到③步应按同分母分式的加减法:分母不变,分子相加减.而不应该把分母去掉;
(3)最简公分母为(x+1)(x-1),通分化简即可.
解答:(1)解:①;
(2)不正确;把分母去掉了;
(3)正确的应是:
-
=
+
=
;
当x=2时,原式=
.
(2)不正确;把分母去掉了;
(3)正确的应是:
| x-3 |
| x2-1 |
| 1 |
| 1-x |
| x-3 |
| (x-1)(x+1) |
| x+1 |
| (x-1)(x+1) |
| 2 |
| x+1 |
当x=2时,原式=
| 2 |
| 3 |
点评:异分母分式相加减,先通分,再按同分母分式法则运算,注意符号的处理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
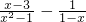 ,其x=2”某同学写出了如下解答:
,其x=2”某同学写出了如下解答: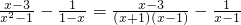
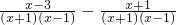
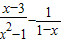 ,其x=2”某同学写出了如下解答:
,其x=2”某同学写出了如下解答: