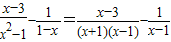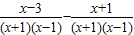题目内容
对于试题:“先化简,再求值:| x-3 |
| x2-1 |
| 1 |
| 1-x |
她的解答正确吗?如不正确,请你写出正确解答.
解:
| x-3 |
| x2-1 |
| 1 |
| 1-x |
| x-3 |
| (x+1)(x-1) |
| 1 |
| x-1 |
=
| x-3 |
| (x+1)(x-1) |
| x+1 |
| (x+1)(x-1) |
=x-3-(x+1)
=x-3+x+1
=2x-2;
当x=2时,原式=2×2-2=2.
分析:本题考查的化简与计算的综合运算,关键是正确进行分式的通分、约分,并准确代值计算.并能准确判断出此题中的错误在哪里,下次做时要特别注意.
解答:解:不正确.
原式=
+
=
=
,
把x=2代入得:
原式=
.
原式=
| x-3 |
| (x+1)(x-1) |
| x+1 |
| (x+1)(x-1) |
| 2x-2 |
| (x+1)(x-1) |
| 2 |
| x+1 |
把x=2代入得:
原式=
| 2 |
| 3 |
点评:本题主要考查分式的化简求值,式子化到最简是解题的关键.

练习册系列答案
相关题目
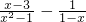 ,其x=2”某同学写出了如下解答:
,其x=2”某同学写出了如下解答: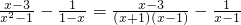
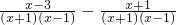
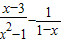 ,其x=2”某同学写出了如下解答:
,其x=2”某同学写出了如下解答: