题目内容
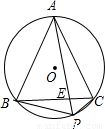
 如图,正△ABC内接于半径为1cm的圆,则阴影部分的面积为
如图,正△ABC内接于半径为1cm的圆,则阴影部分的面积为分析:根据题意作出辅助线,由等边三角形的性质作出△ABC的外心,再设出等边三角形的边长,由垂径定理得出BD=
,再根据特殊角的三角函数即可求出BC及AD的长,根据S阴影=S圆-S△ABC进行计算即可.
| BC |
| 2 |
解答: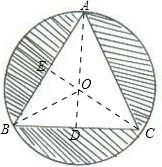 解:分别过A、C作BC、AB边的垂线相交于点O,
解:分别过A、C作BC、AB边的垂线相交于点O,
由等边三角形的性质可知,点O即为△ABC的外心,连接OB则∠OBD=30°,
设正△ABC的边长为a,则
a=1,a=
,
故AD=AB•sin60°=
×
=
,
于是阴影部分的面积为π•12-
×
×
=π•12-
•(
)2=(π-
)(cm2).
故答案为:π-
.
 解:分别过A、C作BC、AB边的垂线相交于点O,
解:分别过A、C作BC、AB边的垂线相交于点O,由等边三角形的性质可知,点O即为△ABC的外心,连接OB则∠OBD=30°,
设正△ABC的边长为a,则
| ||
| 3 |
| 3 |
故AD=AB•sin60°=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
于是阴影部分的面积为π•12-
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 4 |
| 3 |
3
| ||
| 4 |
故答案为:π-
3
| ||
| 4 |
点评:本题考查的是正多边形和圆、特殊角的三角函数值及三角形的面积、圆的面积公式,作出辅助线,利用正三角形的性质得出△ABC的外心是解答此题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
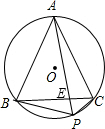 如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:①PA=PB+PC;②
如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:①PA=PB+PC;②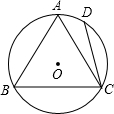 如图,正△ABC内接于⊙O,D是⊙O上一点,∠DCA=15°,CD=10,则BC的长为( )
如图,正△ABC内接于⊙O,D是⊙O上一点,∠DCA=15°,CD=10,则BC的长为( ) ;③PA•PE=PB•PC.其中,正确结论的个数为( )
;③PA•PE=PB•PC.其中,正确结论的个数为( )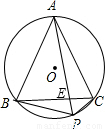
 ;③PA•PE=PB•PC.其中,正确结论的个数为( )
;③PA•PE=PB•PC.其中,正确结论的个数为( )