题目内容
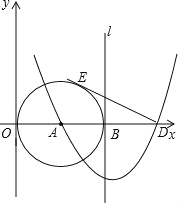
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求此切线长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长.
【答案】(1)![]()
(2)![]()
(3)BF的长为![]() 或
或![]() .
.
【解析】
试题分析:(1)已知了抛物线的顶点坐标,可将抛物线的解析式设为顶点坐标式,然后将C点坐标代入求解即可.
(2)由于DE是⊙A的切线,连接AE,那么根据切线的性质知AE⊥DE,在Rt△AED中,AE、AB是圆的半径,即AE=OA=AB=3,而A、D关于抛物线的对称轴对称,即AB=BD=3,由此可得到AD的长,进而可利用勾股定理求得切线DE的长.
(3)若△BFD与EAD△相似,则有两种情况需要考虑:①△AED∽△BFD,②△AED∽△FBD,根据不同的相似三角形所得不同的比例线段即可求得BF的长.
试题解析:(1)设抛物线的解析式为y=a(x﹣6)2+k;
∵抛物线经过点A(3,0)和C(0,9),
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.
(2)连接AE;
∵DE是⊙A的切线,
∴∠AED=90°,AE=3,
∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,
∴AB=BD=3,
∴AD=6;
在Rt△ADE中,DE2=AD2﹣AE2=62﹣32=27,
∴![]() .
.
(3)当BF⊥ED时;
∵∠AED=∠BFD=90°,∠ADE=∠BDF,
∴△AED∽△BFD,
∴![]() ,
,
即![]() ,
,
∴![]() ;
;
当FB⊥AD时,
∵∠AED=∠FBD=90°,∠ADE=∠FDB,
∴△AED∽△FBD,
∴![]() ,
,
即![]() ;
;
∴BF的长为![]() 或
或![]() .
.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目